Question

【题目】如图，在平面直角坐标系中，OA⊥OB，AB⊥x轴于点C，点A（ ，1）在反比例函数y= 的图象上．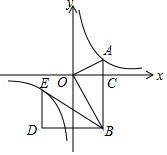

（1）求k的值；
（2）若将△BOA绕点B按逆时针方向旋转60°，得到△BDE，判断点E是否在该反比例函数的图象上，并说明理由．

Answer 1

【答案】
（1）

解：∵点A（ ，1）在反比例函数y= 的图象上，

∴k= ×1=

（2）

解：点E在该反比例函数的图象上，理由如下：

∵A（ ，1），

∴OA= =2，

由OA⊥OB，AB⊥x轴，易证△AOC∽△ABO，

∴ = ，即 = ，

∴AB=4，

∴OB= =2 ，

∴sin∠ABO= = = ，

∴∠ABO=30°．

∵将△BOA绕点B按逆时针方向旋转60°得到△BDE，

∴△BOA≌△BDE，∠OBD=60°，

∴BO=BD=2 ，OA=DE=2，∠BOA=∠BDE=90°，

∠ABD=30°+60°=90°．

又BD﹣OC=2 ﹣ = ，BC﹣DE=4﹣1﹣2=1，

∴E（﹣ ，﹣1），

∵﹣ × ，

∴点E在该反比例函数的图象上

【解析】（1）将点A（ ，1）代入y= ，利用待定系数法即可求出反比例函数的表达式；（2）先解△OAB，得出∠ABO=30°，再根据旋转的性质求出E点坐标为（﹣ ，﹣1），即可求解．