【题目】阅读材料,解决问题:
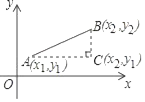
如图,为了求平面直角坐标系中任意两点A(x1,y1)、B(x2,y2)之间的距离,可以AB为斜边作Rt△ABC,则点C的坐标为C(x2,y1),于是AC=|x1﹣x2|,BC=|y1﹣y2|,根据勾股定理可得AB=![]() ,反之,可以将代数式
,反之,可以将代数式![]() 的值看做平面内点(x1,y1)到点(x2,y2)的距离.
的值看做平面内点(x1,y1)到点(x2,y2)的距离.
例如∵![]() =
=![]() =
=![]() ,可将代数式
,可将代数式![]() 看作平面内点(x,y)到点(﹣1,3)的距离
看作平面内点(x,y)到点(﹣1,3)的距离
根据以上材料解决下列问题
(1)求平面内点M(2,﹣3)与点N(﹣1,3)之间的距离;
(2)求代数式![]() 的最小值.
的最小值.
参考答案:
【答案】(1)3![]() (2)2
(2)2![]()
【解析】
(1)依据两点间的距离公式进行计算即可;
(2)先将原式变形,即可将原式可以看作点P(x,y)到点(3,4)和点(﹣5,2)的距离之和,求得AB的长,即可得到该代数式的最小值.
(1)MN=![]() =3
=3![]() ;
;
(2)∵原式=![]() =
=![]() +
+![]() ,
,
∴原式可以看作点P(x,y)到点(3,4)和点(﹣5,2)的距离之和,
∴当点P(x,y)在线段AB上时,原式有最小值,
∵AB=![]() =
=![]() ,
,
∴原式的最小值为2![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学九(5)班为了了解全班学生喜欢球类活动的情况,采取全面调查的方法,从足球、乒乓球、篮球、排球等四个方面调查了全班学生的兴趣爱好,根据调查的结果组建了4个兴趣小组,并绘制成如下的两幅不完整的统计图(如图①,②,要求每位学生只能选择一种自己喜欢的球类),请你根据图中提供的信息解答下列问题:
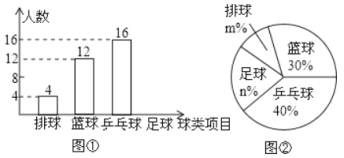
(1)九(5)班的学生人数为_________,并把条形统计图补充完整;
(2)扇形统计图中n=__________,m=___________;
(3)排球兴趣小组4名学生中有2男2女,现在打算从中随机选出2名学生参加学校的排球队,请用列表或画树状图的方法求选出的2名学生恰好是一男一女的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,点F是边BC的中点,连接AF并延长交DC的延长线于点E,连接AC、BE.
中,点F是边BC的中点,连接AF并延长交DC的延长线于点E,连接AC、BE.(1)求证:AB=CE;
(2)若
 ,则四边形ABEC是什么特殊四边形?请说明理由.
,则四边形ABEC是什么特殊四边形?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=BC,以AB为直径的⊙O与AC交于点D,过D作DF⊥BC, 交AB的延长线于E,垂足为F.
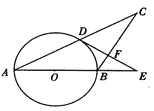
(1)求证:直线DE是⊙O的切线;
(2)当AB=5,AC=8时,求cosE的值.
-
科目: 来源: 题型:
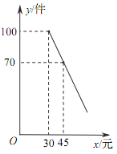
查看答案和解析>>【题目】某商店购进一批成本为每件 30 元的商品,经调查发现,该商品每天的销售量 y(件)与销售单价 x(元)之间满足一次函数关系,其图象如图所示.
(1)求该商品每天的销售量 y 与销售单价 x 之间的函数关系式;
(2)若商店按单价不低于成本价,且不高于 50 元销售,则销售单价定为多少,才能使销售该商品每天获得的利润 w(元)最大?最大利润是多少?
(3)若商店要使销售该商品每天获得的利润不低于 800 元,则每天的销售量最少应为多少件?
-
科目: 来源: 题型:
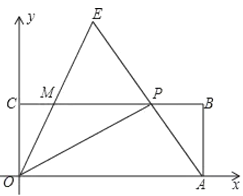
查看答案和解析>>【题目】如图,在直角坐标系xOy中,矩形OABC的顶点A、C分别在x轴和y轴正半轴上,点B的坐标是(5,2),点P是CB边上一动点(不与点C、点B重合),连结OP、AP,过点O作射线OE交AP的延长线于点E,交CB边于点M,且∠AOP=∠COM,令CP=x,MP=y.
(1)求y与x的函数关系式,并写出x的取值范围;
(2)当x为何值时,OP⊥AP?
(3)在点P的运动过程中,是否存在x,使△OCM的面积与△ABP的面积之和等于△EMP的面积?若存在,请求x的值;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为纪念建国70周年,某校举行班级歌咏比赛,歌曲有:《我爱你,中国》,《歌唱祖国》,《我和我的祖国》(分别用字母A,B,C依次表示这三首歌曲).比赛时,将A,B,C这三个字母分别写在3张无差别不透明的卡片正面上,洗匀后正面向下放在桌面上,八(1)班班长先从中随机抽取一张卡片,放回后洗匀,再由八(2)班班长从中随机抽取一张卡片,进行歌咏比赛.
(1)八(1)班抽中歌曲《我和我的祖国》的概率是__________;
(2)试用画树状图或列表的方法表示所有可能的结果,并求出八(1)班和八(2)班抽中不同歌曲的概率.
相关试题

