【题目】某中学九(5)班为了了解全班学生喜欢球类活动的情况,采取全面调查的方法,从足球、乒乓球、篮球、排球等四个方面调查了全班学生的兴趣爱好,根据调查的结果组建了4个兴趣小组,并绘制成如下的两幅不完整的统计图(如图①,②,要求每位学生只能选择一种自己喜欢的球类),请你根据图中提供的信息解答下列问题:
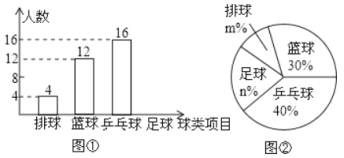
(1)九(5)班的学生人数为_________,并把条形统计图补充完整;
(2)扇形统计图中n=__________,m=___________;
(3)排球兴趣小组4名学生中有2男2女,现在打算从中随机选出2名学生参加学校的排球队,请用列表或画树状图的方法求选出的2名学生恰好是一男一女的概率.
参考答案:
【答案】(1)40;图见解析 (2)10;20 (3)![]()
【解析】
(1)根据喜欢篮球的人数与所占的百分比列式计算即可求出学生的总人数,再求出喜欢足球的人数,然后补全统计图即可;
(2)分别求出喜欢排球、喜欢足球的百分比即可得到m、n的值;
(3)画出树状图,然后根据概率公式列式计算即可得解.
解:(1)九(5)班的学生人数为:12÷30%=40(人),
喜欢足球的人数为:4041216=4032=8(人),
补全统计图如图所示;
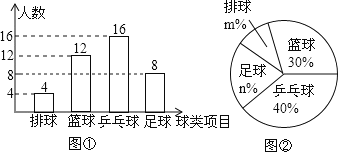
(2)∵![]() ×100%=10%,
×100%=10%,
![]() ×100%=20%,
×100%=20%,
∴m=10,n=20,
(3)根据题意画出树状图如下:
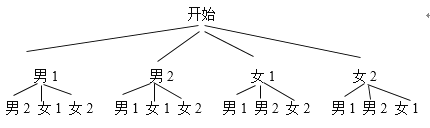
一共有12种情况,恰好是1男1女的情况有8种,
∴P(恰好是1男1女)=![]() =
=![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在矩形ABCD中,点P是BC边上一点,连接AP交对角线BD于点E,
 .作线段AP的中垂线MN分别交线段DC,DB,AP,AB于点M,G,F,N.
.作线段AP的中垂线MN分别交线段DC,DB,AP,AB于点M,G,F,N.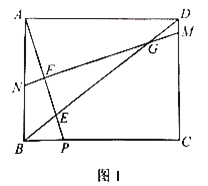
(1)求证:
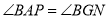 ;
;(2)若
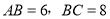 ,求
,求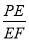 .
.(3)如图2,在(2)的条件下,连接CF,求
 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=ax2+bx+c的图象与x轴交于点A(﹣1,0),B(3,0).下列结论:①2a﹣b=0;②(a+c)2<b2;③当﹣1<x<3时,y<0;④当a=1时,将抛物线先向上平移2个单位,再向右平移1个单位,得到抛物线y=(x﹣2)2﹣2.其中正确的是( )
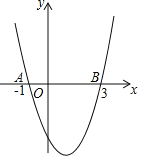
A. ①③ B. ②③ C. ②④ D. ③④
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=x2+2x﹣3与x轴交于A,B两点(点A在点B的左侧),将这条抛物线向右平移m(m>0)个单位长度,平移后的抛物线与x轴交于C,D两点(点C在点D的左侧),若B,C是线段AD的三等分点,则m的值为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,点F是边BC的中点,连接AF并延长交DC的延长线于点E,连接AC、BE.
中,点F是边BC的中点,连接AF并延长交DC的延长线于点E,连接AC、BE.(1)求证:AB=CE;
(2)若
 ,则四边形ABEC是什么特殊四边形?请说明理由.
,则四边形ABEC是什么特殊四边形?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=BC,以AB为直径的⊙O与AC交于点D,过D作DF⊥BC, 交AB的延长线于E,垂足为F.
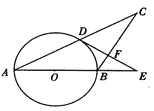
(1)求证:直线DE是⊙O的切线;
(2)当AB=5,AC=8时,求cosE的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料,解决问题:
如图,为了求平面直角坐标系中任意两点A(x1,y1)、B(x2,y2)之间的距离,可以AB为斜边作Rt△ABC,则点C的坐标为C(x2,y1),于是AC=|x1﹣x2|,BC=|y1﹣y2|,根据勾股定理可得AB=
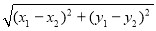 ,反之,可以将代数式
,反之,可以将代数式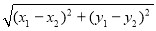 的值看做平面内点(x1,y1)到点(x2,y2)的距离.
的值看做平面内点(x1,y1)到点(x2,y2)的距离.例如∵
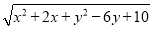 =
=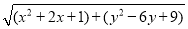 =
=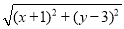 ,可将代数式
,可将代数式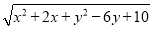 看作平面内点(x,y)到点(﹣1,3)的距离
看作平面内点(x,y)到点(﹣1,3)的距离根据以上材料解决下列问题
(1)求平面内点M(2,﹣3)与点N(﹣1,3)之间的距离;
(2)求代数式
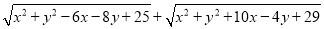 的最小值.
的最小值.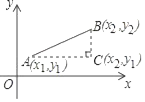
相关试题

