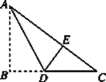
【题目】如图,有一块直角三角形纸片,两直角边AB=6,BC=8,将△ABC折叠,使AB落在斜边AC上,折痕为AD,则BD的长为( )

A. 6B. 5C. 4D. 3
参考答案:
【答案】D
【解析】
设点B落在AC上的E点处,连接DE,如图所示,由三角形ABC为直角三角形,由AB与BC的长,利用勾股定理求出AC的长,设BD=x,由折叠的性质得到ED=BD=x,AE=AB=6,进而表示出CE与CD,在直角三角形DEC中,利用勾股定理列出关于x的方程,求出方程的解得到x的值,即可确定出BD的长.
解:∵△ABC为直角三角形,AB=6,BC=8,
∴根据勾股定理得:![]() ,
,
设BD=x,由折叠可知:ED=BD=x,AE=AB=6,
可得:CE=AC-AE=10-6=4,CD=BC-BD=8-x,
在Rt△CDB'中,
根据勾股定理得:(8-x)2=42+x2,
解得:x=3,
则BD=3.
故答案为:3.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=2x+6交x轴于A,交y轴于B.

(1)直接写出A( , ),B( , );
(2)如图1,点E为直线y=x+2上一点,点F为直线y=
 x上一点,若以A,B,E,F为顶点的四边形是平行四边形,求点E,F的坐标
x上一点,若以A,B,E,F为顶点的四边形是平行四边形,求点E,F的坐标(3)如图2,点C(m,n)为线段AB上一动点,D(﹣7m,0)在x轴上,连接CD,点M为CD的中点,求点M的纵坐标y和横坐标x之间的函数关系式,并直接写出在点C移动过程中点M的运动路径长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店欲购进甲、乙两种商品,已知甲的进价是乙的进价的一半,进3件甲商品和1件乙商品恰好用200元.甲、乙两种商品的售价每件分别为80元、130元,该商店决定用不少于6710元且不超过6810元购进这两种商品共100件.
(1)求这两种商品的进价.
(2)该商店有几种进货方案?哪种进货方案可获得最大利润,最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学计划购买A型和B型课桌凳共200套,经招标,购买一套A型课桌凳比购买一套B型课桌凳少用40元,,且购买4套A型和6套B型课桌凳共需1820元。
(1)求购买一套A型课桌凳和一套B型课桌凳各需多少元?
(2)学校根据实际情况,要求购买这两种课桌凳总费用不能超过40880元,并且购买A型课桌凳的数量不能超过B型课桌凳的
 ,求该校本次购买A型和B型课桌凳共有几种方案?哪种方案的总费用最低?
,求该校本次购买A型和B型课桌凳共有几种方案?哪种方案的总费用最低? -
科目: 来源: 题型:
查看答案和解析>>【题目】下图反映的过程是小明从家去菜地浇水,又去玉米地锄草,然后回家.其中x表示时间,y表示小明离他家的距离.根据图象回答下列问题:

①菜地离小明家多远?小明走到菜地用了多少时间?
②小明给菜地浇水用了多少时间?
③玉米地离菜地、小明家多远?小明从玉米地走回家平均速度是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校实行学案式教学,需印制若干份教学学案.印刷厂有,甲、乙两种收费方式,除按印数收取印刷费外,甲种方式还需收取制版费而乙种不需要,两种印刷方式的费用y(元)与印刷份数x(份)之间的关系如图所示.

(1)填空:甲种收费方式的函数关系式是__________,乙种收费方式的函数关系式是__________.
(2)该校某年级每次需印制100~450(含100和450)份学案,选择哪种印刷方式较合算.
-
科目: 来源: 题型:
查看答案和解析>>【题目】建设环境优美、文明和谐的新农村,某村村委会决定在村道两旁种植A,B两种树木,需要购买这两种树苗1000棵.A,B两种树苗的相关信息如下表:
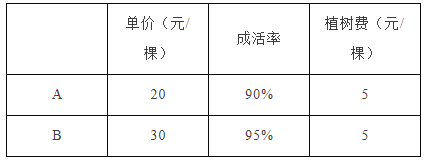
设购买A种树苗x棵,绿化村道的总费用为y元.解答下列问题:
(1)写出y(元)与x(棵)之间的函数关系式;
(2)若这批树苗种植后成活了925棵,则绿化村道的总费用需要多少元?
(3)若绿化村道的总费用不超过31000元,则最多可购买B种树苗多少棵?
相关试题

