【题目】某商店欲购进甲、乙两种商品,已知甲的进价是乙的进价的一半,进3件甲商品和1件乙商品恰好用200元.甲、乙两种商品的售价每件分别为80元、130元,该商店决定用不少于6710元且不超过6810元购进这两种商品共100件.
(1)求这两种商品的进价.
(2)该商店有几种进货方案?哪种进货方案可获得最大利润,最大利润是多少?
参考答案:
【答案】(1)商品的进价为40元,乙商品的进价为80元.
(2)有三种进货方案:
方案1,甲种商品30件,乙商品70件;
方案2,甲种商品31件,乙商品69件;
方案3,甲种商品32件,乙商品68件.
方案1可获得最大利润,最大=4700.
【解析】
(1)设甲商品的进价为x元,乙商品的进价为y元,就有![]() ,3x+y=200,由这两个方程构成方程组求出其解即可.
,3x+y=200,由这两个方程构成方程组求出其解即可.
(2)设购进甲种商品m件,则购进乙种商品(100﹣m)件,根据不少于6710元且不超过6810元购进这两种商品100的货款建立不等式,求出其值就可以得出进货方案,设利润为W元,根据利润=售价﹣进价建立解析式就可以求出结论.
解:(1)设甲商品的进价为x元,乙商品的进价为y元,由题意,得
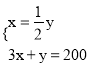 ,解得:
,解得:![]() .
.
答:商品的进价为40元,乙商品的进价为80元.
(2)设购进甲种商品m件,则购进乙种商品(100﹣m)件,由题意,得
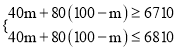 ,解得:
,解得:![]() .
.
∵m为整数,∴m=30,31,32.
∴有三种进货方案:
方案1,甲种商品30件,乙商品70件;
方案2,甲种商品31件,乙商品69件;
方案3,甲种商品32件,乙商品68件.
设利润为W元,由题意,得![]() ,
,
∵k=﹣10<0,∴W随m的增大而减小.
∴m=30时,W最大=4700.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,五个正方形面积分别记为S1,S2,S3,S4,S5,若S1=2,S3=3,S5=5,则S2+S4=_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】探究:如图①,在△ABC 中,∠BAC=90°,AB=AC,直线 m 经过点 A,BD⊥m 于点 D,CE⊥m 于点 E,求证:△ABD≌△CAE.
应用:如图②,在△ABC 中,AB=AC,D、A、E 三点都在直线 m 上,并且有∠BDA=∠AEC=∠BAC,求证:DE=BD+CE.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某电台“市民热线”对上周内接到的热线电话进行了分类统计,得到的统计信息图如图所示,其中有关房产城建的电话有30个,请你根据统计图的信息回答以下问题:
(1)道路交通热线电话是多少个占总数百分比是多少?
(2)上周“市民热线”接到有关环境保护方面的电话有多少个?
(3)据此估计,除环境保护方面的电话外,“市民热线”今年(按52周计算)将接到的热线电话约多少个?
(4)为了更直观显示各类“市民热线”电话的数目,你准备采用什么样的统计方法?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC中,AB=AC=20cm,BC=16cm,D为AB中点,如果点P在线段BC上由点B出发向点C运动,同时点Q在线段CA上由点C出发向点A运动,设运动时间为t(s).
(1)若点P与点Q的速度都是2cm/s,问经过多少时间△BPD与△CQP全等?说明理由;
(2)若点P的速度比点Q的速度都慢2cm/s,则经过多少时间△BPD与△CQP全等,并求出此时两点的速度;
(3)若点P、点Q分别以(2)中速度同时从B、C出发,都逆时针沿△ABC三边运动,问经过多少时间点P与点Q第一次相遇,相遇点在△ABC的哪条边上?并求出相遇点与点B的距离.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD为正方形,边长为4,点F在AB边上,E为射线AD上一点,正方形ABCD沿直线EF折叠,点A落在G处,已知点G恰好在以AB为直径的圆上,则CG的最小值等于( )

A.0
B.2
C.4﹣2
D.2 ﹣2
﹣2 -
科目: 来源: 题型:
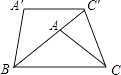
查看答案和解析>>【题目】如图,将△ABC绕点B逆时针旋转40°,得到△A′B′C′,若点C′恰好落在边BA的延长线上,且A′C′∥BC,连接CC′,则∠ACC′=度.
相关试题

