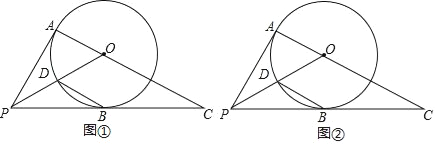
【题目】已知PA、PB是⊙O的切线,A、B为切点,连接AO并延长,交PB的延长线于点C,连接PO,交⊙O于点D.
(1)如图①,若∠AOP=65°,求∠C的大小;
(2)如图②,连接BD,若BD∥AC,求∠C的大小.
参考答案:
【答案】(1)40°;(2)30°.
【解析】
(1) 连接OB,根据切线长定理可知∠APO=∠BPO=25,利用三角形的外角性质求出∠C.
(2)连接OB,先利用BD∥AC,说明△OBD是等边三角形,得出∠BOP=∠AOP=60,∠APO=30,利用三角形的外角性质求出∠C.
解:(1)连接BO,
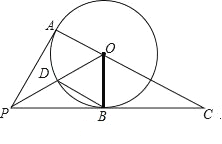
∵PA、PB是⊙O的切线,
∴∠APO=∠BPO,PA⊥AO,PB⊥OB,
∵∠AOP=65°,
∴∠APO=90°﹣65°=25°,
∴∠BPO=∠APO=25°,
∵∠AOP=∠BPO+∠C,
∴∠C=∠AOP﹣∠BPO=65°﹣25°=40°,
(2)连接OB,设∠AOP=x,

∵PA、PB是⊙O的切线,
∴∠APO=∠BPO,PA⊥AO,PB⊥OB,
∴∠AOP=∠BOP,OA=OB=OD,
∵BD∥AC,
∴∠ODB=∠AOP,
∴∠ODB=∠BOP,即∠ODB=∠BOD,
∴BD=OB=OD,
∴△OBD是等边三角形,
∴∠BOP=∠AOP=60,
∴∠BPO=30,
∴∠C=∠AOP-∠BPO=30.
故答案为:(1)40°;(2)30°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知锐角∠AOB如图,(1)在射线OA上取一点C,以点O为圆心,OC长为半径作
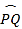 ,交射线OB于点D,连接CD;
,交射线OB于点D,连接CD;(2)分别以点C,D为圆心,CD长为半径作弧,交
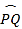 于点M,N;
于点M,N;(3)连接OM,MN.
根据以上作图过程及所作图形,下列结论中错误的是( )

A. ∠COM=∠CODB. 若OM=MN,则∠AOB=20°
C. MN∥CDD. MN=3CD
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是学习“分式方程应用”时,老师板书的例题和两名同学所列的方程.
15.3分式方程
例:有甲、乙两个工程队,甲队修路
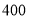 米与乙队修路
米与乙队修路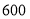 米所用时间相等.乙队每天比甲队多修
米所用时间相等.乙队每天比甲队多修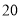 米,求甲队每天修路的长度.
米,求甲队每天修路的长度.冰冰:
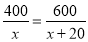
庆庆:
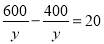
根据以上信息,解答下列问题:
(1)冰冰同学所列方程中的
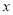 表示_____,庆庆同学所列方 程中的
表示_____,庆庆同学所列方 程中的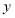 表示;
表示;(2)两个方程中任选一个,写出它的等量关系;
(3)解(2)中你所选择的方程,并解答老师的例题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数学活动课上,李老师让同学们试着用角尺平分
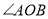 (如图所示),有两组.
(如图所示),有两组.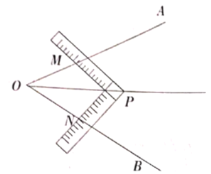
同学设计了如下方案:
方案①:将角尺的直角顶点
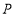 介于射线
介于射线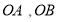 之间,移动角尺使角尺两边相同的刻度位于
之间,移动角尺使角尺两边相同的刻度位于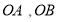 上,且交点分别为
上,且交点分别为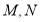 ,即
,即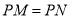 ,过角尺顶点
,过角尺顶点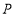 的射线
的射线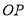 就是
就是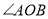 的平分线.
的平分线.方案②:在边
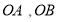 上分别截取
上分别截取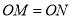 ,将角尺的直角顶点
,将角尺的直角顶点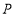 介于射线
介于射线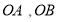 之间,移动角尺使角尺两边相同的刻度与点
之间,移动角尺使角尺两边相同的刻度与点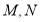 重合,即
重合,即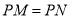 ,过角尺顶点
,过角尺顶点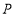 的射线
的射线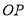 就是
就是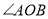 的平分线.请分别说明方案①与方案②是否可行?若可行,请证明; 若不可行,请说明理由.
的平分线.请分别说明方案①与方案②是否可行?若可行,请证明; 若不可行,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】综合与探究
[问题]如图1,在
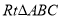 中,
中,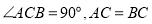 ,过点
,过点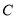 作直线
作直线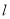 平行于
平行于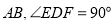 ,点
,点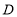 在直线
在直线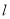 上移动,角的一边DE始终经过点
上移动,角的一边DE始终经过点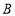 ,另一边
,另一边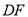 与
与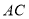 交于点
交于点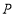 ,研究
,研究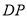 和
和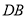 的数量关系.
的数量关系.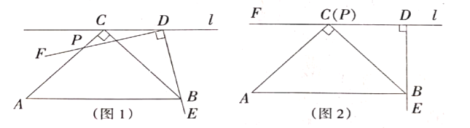
[探究发现]
(1)如图2,某数学学习小组运用“从特殊到一般”的数学思想,发现当点
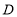 移动到使点
移动到使点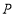 与点
与点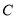 重合时,很容易就可以得到
重合时,很容易就可以得到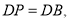 请写出证明过程;
请写出证明过程;[数学思考]
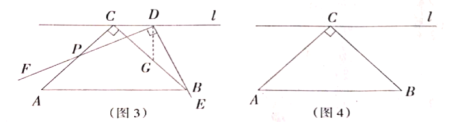
(2)如图3,若点
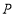 是
是 上的任意一点(不含端点
上的任意一点(不含端点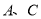 ),受(1)的启发,另一个学习小组过点
),受(1)的启发,另一个学习小组过点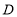 ,
,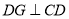 交
交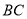 于点
于点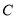 ,就可以证明
,就可以证明 ,请完成证明过程;
,请完成证明过程;[拓展引申]
(3)若点
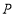 是
是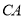 延长线上的任意一点,在图(4)中补充完整图形,并判断结论是否仍然成立.
延长线上的任意一点,在图(4)中补充完整图形,并判断结论是否仍然成立. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,学校的实验楼对面是一幢教学楼,小敏在实验楼的窗口C处测得教学楼顶部D处的仰角为18°,教学楼底部B处的俯角为20°,教学楼的高BD=21m,求实验楼与教学楼之间的距离AB(结果保留整数).(参考数据:tan18°≈0.32,tan20°≈0.36)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
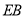 交
交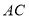 于点
于点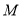 ,交
,交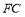 于点
于点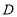 ,
,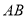 交
交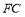 于点
于点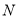 ,
,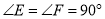 ,
,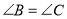 ,
,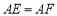 ,给出下列结论:①
,给出下列结论:①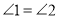 ;②
;②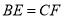 ;③
;③ ;④
;④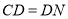 ;⑤
;⑤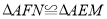 .其中正确的结论有( )
.其中正确的结论有( )
A.2个B.3个C.4个D.5个
相关试题

