【题目】如图,![]() 交
交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,
,![]() 交
交![]() 于点
于点![]() ,
,![]() ,
,![]() ,
,![]() ,给出下列结论:①
,给出下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() .其中正确的结论有( )
.其中正确的结论有( )

A.2个B.3个C.4个D.5个
参考答案:
【答案】C
【解析】
根据∠E=∠F=90°,∠B=∠C,AE=AF可得△ABE≌△ACF,可得②BE=CF;∠BAE=∠CAF可得①∠1=∠2;由ASA可得③△ACN≌△ABM,⑤![]() .④CD=DN不成立.
.④CD=DN不成立.
由已知条件,可直接得到三角形全等,得到结论,采用排除法,对各个选项进行验证从而确定正确的结论.
解:∵![]()
∴∠B+∠BAE=90°,∠C+∠CAF=90°,∠B=∠C
∴∠1=∠2(①正确)
∵∠E=∠F=90°,AE=AF,∠B=∠C
∴△ABE≌△ACF(ASA)
∴AB=AC,BE=CF(②正确)
∵∠CAN=∠BAM,∠B=∠C,AB=AC
∴△ACN≌△ABM(③正确)
∴CN=BM(④不正确).
∵∠1=∠2,AE=AF,∠E=∠F
∴△AFN≌△AEM(⑤正确)
所以正确结论有①②③⑤.
故选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知PA、PB是⊙O的切线,A、B为切点,连接AO并延长,交PB的延长线于点C,连接PO,交⊙O于点D.
(1)如图①,若∠AOP=65°,求∠C的大小;
(2)如图②,连接BD,若BD∥AC,求∠C的大小.
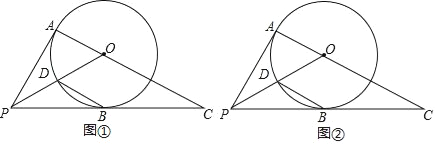
-
科目: 来源: 题型:
查看答案和解析>>【题目】综合与探究
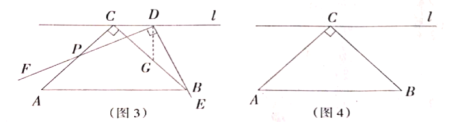
[问题]如图1,在
 中,
中,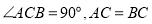 ,过点
,过点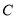 作直线
作直线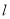 平行于
平行于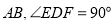 ,点
,点 在直线
在直线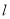 上移动,角的一边DE始终经过点
上移动,角的一边DE始终经过点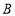 ,另一边
,另一边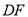 与
与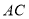 交于点
交于点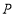 ,研究
,研究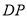 和
和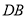 的数量关系.
的数量关系.
[探究发现]
(1)如图2,某数学学习小组运用“从特殊到一般”的数学思想,发现当点
 移动到使点
移动到使点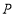 与点
与点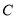 重合时,很容易就可以得到
重合时,很容易就可以得到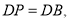 请写出证明过程;
请写出证明过程;[数学思考]
(2)如图3,若点
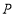 是
是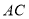 上的任意一点(不含端点
上的任意一点(不含端点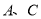 ),受(1)的启发,另一个学习小组过点
),受(1)的启发,另一个学习小组过点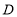 ,
,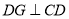 交
交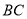 于点
于点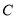 ,就可以证明
,就可以证明 ,请完成证明过程;
,请完成证明过程;[拓展引申]
(3)若点
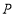 是
是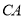 延长线上的任意一点,在图(4)中补充完整图形,并判断结论是否仍然成立.
延长线上的任意一点,在图(4)中补充完整图形,并判断结论是否仍然成立. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,学校的实验楼对面是一幢教学楼,小敏在实验楼的窗口C处测得教学楼顶部D处的仰角为18°,教学楼底部B处的俯角为20°,教学楼的高BD=21m,求实验楼与教学楼之间的距离AB(结果保留整数).(参考数据:tan18°≈0.32,tan20°≈0.36)

-
科目: 来源: 题型:
查看答案和解析>>【题目】某共享单车公司提供了手机和会员卡两种支付方式.若用手机支付方式,骑行时间在半小时以内(含半小时)不收费,超出半小时后每半小时收费1元,若选择会员卡支付,骑行时间每半小时收费0.8元,设骑行时间为x小时.
(1)根据题意,填写下表(单位:元):
骑行时间(小时)
0.5
2
3
…
手机支付付款金额(元)
0
…
会员卡支付付款金额(元)
3.2
…
(2)设用手机支付付款金额为y1元,用会员卡支付付款金额为y2元,分别写出y1,y2关于x的函数关系式;
(3)若李老师经常骑行该公司的共享单车,他应选择哪种支付方式比较合算?
-
科目: 来源: 题型:
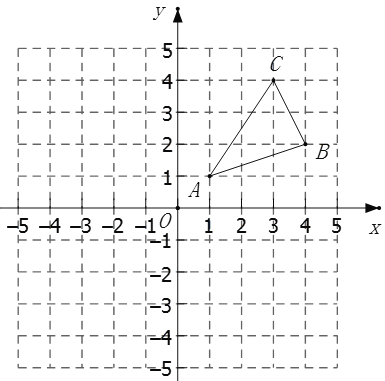
查看答案和解析>>【题目】如图,
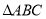 三个顶点的坐标分别为
三个顶点的坐标分别为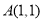 ,
,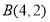 ,
,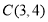 .
.
(1)请画出
 关于
关于 轴成轴对称的图形
轴成轴对称的图形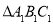 ,并写出
,并写出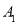 、
、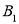 、
、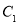 的坐标;
的坐标;(2)求
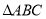 的面积;
的面积;(3〉在
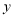 轴上找一点
轴上找一点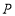 ,使
,使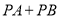 的值最小,请画出点
的值最小,请画出点 的位置.
的位置. -
科目: 来源: 题型:
查看答案和解析>>【题目】将一个直角三角形纸片ABO,放置在平面直角坐标系中,点A(2,0),点B(0,2),点O(0,0).点M为边OA上的一个动点(点M不与点O、A重合),沿着BM折叠该纸片,得顶点O的对应点O′.
(I)如图①,当点O′在边AB上时,求点O′的坐标;
(II)设直线BO′与x轴相交于点F.
①如图②,当BA平分∠MBF时,求点F的坐标;
②当OM=
 时,求点F的坐标(直接写出结果即可)
时,求点F的坐标(直接写出结果即可)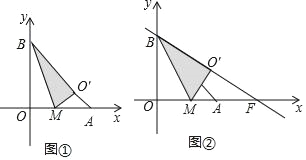
相关试题

