【题目】某学习小组在探究三角形全等时,发现了下面这种典型的基本图形:
![]() 如图1,已知:在
如图1,已知:在![]() 中,
中,![]() ,
,![]() ,直线m经过点A,
,直线m经过点A,![]() 直线m,
直线m,![]() 直线m,垂足分别为点D、
直线m,垂足分别为点D、![]() 试猜想DE、BD、CE有怎样的数量关系,请直接写出;
试猜想DE、BD、CE有怎样的数量关系,请直接写出;
![]() 组员小颖想,如果三个角不是直角,那结论是否会成立呢?如图2,将
组员小颖想,如果三个角不是直角,那结论是否会成立呢?如图2,将![]() 中的条件改为:在
中的条件改为:在![]() 中,
中,![]() ,D、A、E三点都在直线m上,并且有
,D、A、E三点都在直线m上,并且有![]() 其中
其中![]() 为任意锐角或钝角
为任意锐角或钝角![]() 如果成立,请你给出证明;若不成立,请说明理由.
如果成立,请你给出证明;若不成立,请说明理由.
![]() 数学老师赞赏了他们的探索精神,并鼓励他们运用这个知识来解决问题:
数学老师赞赏了他们的探索精神,并鼓励他们运用这个知识来解决问题:
如图3,F是![]() 角平分线上的一点,且
角平分线上的一点,且![]() 和
和![]() 均为等边三角形,D、E分别是直线m上A点左右两侧的动点
均为等边三角形,D、E分别是直线m上A点左右两侧的动点![]() 、E、A互不重合
、E、A互不重合![]() ,在运动过程中线段DE的长度始终为n,连接BD、CE,若
,在运动过程中线段DE的长度始终为n,连接BD、CE,若![]() ,试判断
,试判断![]() 的形状,并说明理由.
的形状,并说明理由.

参考答案:
【答案】![]() ,理由见解析;
,理由见解析;![]() 结论
结论![]() 成立;理由见解析;
成立;理由见解析;![]() 为等边三角形,理由见解析.
为等边三角形,理由见解析.
【解析】
(1)先利用同角的余角相等,判断出![]() ,进而判断△ADB≌△CEA,得出BD=AE,AD=CE,即可得出结论;
,进而判断△ADB≌△CEA,得出BD=AE,AD=CE,即可得出结论;
(2)先利用三角形内角和及平角的性质,判断出![]() ,进而判断出△ADB≌△CEA,得出BD=AE,AD=CE,即可得出结论;
,进而判断出△ADB≌△CEA,得出BD=AE,AD=CE,即可得出结论;
(3)由(2)得,△ADB≌△CEA,得出BD=AE,再判断出△FBD≌△FAE,得出![]() ,进而得出
,进而得出![]() ,即可得出结论.
,即可得出结论.
![]() ,
,
理由:![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,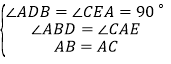 ,
,
![]() ≌
≌![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
故答案为:![]() ;
;
![]() 解:结论
解:结论![]() 成立;
成立;
理由如下:![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,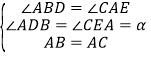 ,
,
![]() ≌
≌![]() ,
,
![]() ,
,![]() ,
,
![]() ;
;
![]() 为等边三角形,
为等边三角形,
理由:由![]() 得,
得,![]() ≌
≌![]() ,
,
![]() ,
,![]() ,
,
![]() ,即
,即![]() ,
,
在![]() 和
和![]() 中,
中,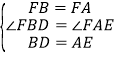 ,
,
![]() ≌
≌![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() 为等边三角形.
为等边三角形.
故答案为:(1)DE=BD+CE,理由见解析;(2)结论DE=BD+CE成立;理由见解析;(3)△DFE为等边三角形,理由见解析.
-
科目: 来源: 题型:
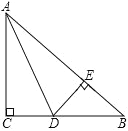
查看答案和解析>>【题目】如图,在
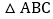 中,
中,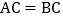 ,
,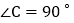 ,AD是
,AD是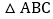 的角平分线,
的角平分线,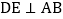 ,垂足为E.
,垂足为E.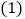 求证:
求证: ;
; 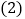 已知
已知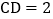 ,求AC的长;
,求AC的长; 求证:
求证: .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】从﹣3,﹣2,﹣1,0,1,2,3这七个数中随机抽取一个数记为a,则a的值是不等式组
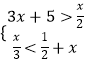 的解,但不是方程x2﹣3x+2=0的实数解的概率为 .
的解,但不是方程x2﹣3x+2=0的实数解的概率为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD中,M、N是BD的三等分点,连接CM并延长交AB于点E,连接EN并延长交CD于点F,以下结论:
①E为AB的中点;
②FC=4DF;
③S△ECF= ;
;
④当CE⊥BD时,△DFN是等腰三角形.
其中一定正确的是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:在直角梯形ABCD中,AD∥BC,∠C=90°,AB=AD=25,BC=32.连接BD,AE⊥BD垂足为E.

(1)求证:△ABE∽△DBC;
(2)求线段AE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,反比例函数y=
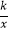 (x>0)的图象经过点A(1,2)和点B(m,n)(m>1),过点B作y轴的垂线,垂足为C.
(x>0)的图象经过点A(1,2)和点B(m,n)(m>1),过点B作y轴的垂线,垂足为C.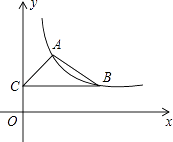
(1)求该反比例函数解析式;
(2)当△ABC面积为2时,求点B的坐标.
(3)P为线段AB上一动点(P不与A、B重合),在(2)的情况下,直线y=ax﹣1与线段AB交于点P,直接写出a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】王师傅非常喜欢自驾游,为了解他新买的轿车的耗油情况,将油箱加满后进行了耗油实验,得到下表中的数据:
轿车行驶的路程
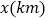
0
100
200
300
400
油箱中的剩余油量
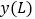
50
42
34
26
18
(1)在这个问题中,自变量是 ,因变量是 ;
(2)该轿车油箱的容量为
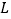 ,行驶
,行驶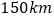 时,估计油箱中的剩余油量为
时,估计油箱中的剩余油量为 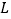 ;
;(3)王师傅将油箱加满后,驾驶该轿车从
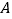 地前往
地前往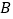 地,到达
地,到达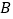 地时油箱中的剩余油量为
地时油箱中的剩余油量为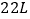 ,请直接写出
,请直接写出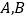 两地之间的距离是
两地之间的距离是 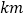 .
.
相关试题

