【题目】王师傅非常喜欢自驾游,为了解他新买的轿车的耗油情况,将油箱加满后进行了耗油实验,得到下表中的数据:
轿车行驶的路程 | 0 | 100 | 200 | 300 | 400 |
油箱中的剩余油量 | 50 | 42 | 34 | 26 | 18 |
(1)在这个问题中,自变量是 ,因变量是 ;
(2)该轿车油箱的容量为 ![]() ,行驶
,行驶![]() 时,估计油箱中的剩余油量为
时,估计油箱中的剩余油量为 ![]() ;
;
(3)王师傅将油箱加满后,驾驶该轿车从![]() 地前往
地前往![]() 地,到达
地,到达![]() 地时油箱中的剩余油量为
地时油箱中的剩余油量为![]() ,请直接写出
,请直接写出![]() 两地之间的距离是
两地之间的距离是 ![]() .
.
参考答案:
【答案】(1)轿车行驶的路程![]() ,邮箱中的剩余油量
,邮箱中的剩余油量![]() ;(2)50,38;(3)350.
;(2)50,38;(3)350.
【解析】
(1)由表格可知,油箱的余油量随着行驶路程的变化而变化,而且对于确定的路程数,剩余油量有唯一确定的值,由此即可得答案;
(2)由表格可知,开始油箱中的油为50L,每行驶100km,油量减少8L,据此可得y与x的关系式,把x=150代入关系式即可求得答案;
(3)把y=22代入函数关系式求得相应的y值即可.
(1)由表格可知,油箱的余油量随着行驶路程的变化而变化,而且对于确定的路程数,剩余油量有唯一确定的值,所以这个问题中,自变量是轿车行驶的路程x,因变量是油箱中剩余油量y,
故答案为:轿车行驶的路程![]() ,油箱中的剩余油量
,油箱中的剩余油量![]() ;
;
(2)由表格可知,开始油箱中的油为50L,每行驶100km,油量减少8L,据此可得y与x的关系式为y=50-0.08x,
当x=150时,y=50-0.08×150=38,
故答案为:50,38;
(3)令y=22,则50-0.08x=22,
解得x=350,
即A,B两地之间的距离为350km,
故答案为:350.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学习小组在探究三角形全等时,发现了下面这种典型的基本图形:
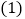 如图1,已知:在
如图1,已知:在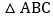 中,
中, ,
,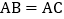 ,直线m经过点A,
,直线m经过点A, 直线m,
直线m,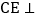 直线m,垂足分别为点D、
直线m,垂足分别为点D、 试猜想DE、BD、CE有怎样的数量关系,请直接写出;
试猜想DE、BD、CE有怎样的数量关系,请直接写出; 组员小颖想,如果三个角不是直角,那结论是否会成立呢?如图2,将
组员小颖想,如果三个角不是直角,那结论是否会成立呢?如图2,将 中的条件改为:在
中的条件改为:在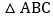 中,
中,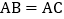 ,D、A、E三点都在直线m上,并且有
,D、A、E三点都在直线m上,并且有 其中
其中 为任意锐角或钝角
为任意锐角或钝角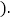 如果成立,请你给出证明;若不成立,请说明理由.
如果成立,请你给出证明;若不成立,请说明理由. 数学老师赞赏了他们的探索精神,并鼓励他们运用这个知识来解决问题:
数学老师赞赏了他们的探索精神,并鼓励他们运用这个知识来解决问题:如图3,F是
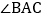 角平分线上的一点,且
角平分线上的一点,且 和
和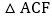 均为等边三角形,D、E分别是直线m上A点左右两侧的动点
均为等边三角形,D、E分别是直线m上A点左右两侧的动点 、E、A互不重合
、E、A互不重合 ,在运动过程中线段DE的长度始终为n,连接BD、CE,若
,在运动过程中线段DE的长度始终为n,连接BD、CE,若 ,试判断
,试判断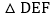 的形状,并说明理由.
的形状,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:在直角梯形ABCD中,AD∥BC,∠C=90°,AB=AD=25,BC=32.连接BD,AE⊥BD垂足为E.

(1)求证:△ABE∽△DBC;
(2)求线段AE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,反比例函数y=
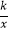 (x>0)的图象经过点A(1,2)和点B(m,n)(m>1),过点B作y轴的垂线,垂足为C.
(x>0)的图象经过点A(1,2)和点B(m,n)(m>1),过点B作y轴的垂线,垂足为C.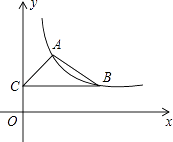
(1)求该反比例函数解析式;
(2)当△ABC面积为2时,求点B的坐标.
(3)P为线段AB上一动点(P不与A、B重合),在(2)的情况下,直线y=ax﹣1与线段AB交于点P,直接写出a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】周末,小明乘坐家门口的公交车到和平公园游玩,他先乘坐公交车0.8小时后达到书城,逗留一段时间后继续坐公交车到和平公园,小明出发一段时间后,小明的妈妈不放心,于是驾车沿相同的路线前往和平公园,如图是他们离家的路程
 与离家时间
与离家时间 的关系图,请根据图回答下列问题:
的关系图,请根据图回答下列问题: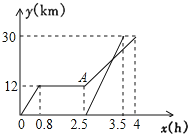
(1)小明家到和平公园的路程为
 ,他在书城逗留的时间为
,他在书城逗留的时间为  ;
;(2)图中
 点表示的意义是 ;
点表示的意义是 ;(3)求小明的妈妈驾车的平均速度(平均速度=
 ).
). -
科目: 来源: 题型:
查看答案和解析>>【题目】已知反比例函数
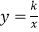 的图象经过点A(1,3).
的图象经过点A(1,3).
(1)试确定此反比例函数的解析式;
(2)当x=2时,求y的值;
(3)当自变量x从5增大到8时,函数值y是怎样变化的? -
科目: 来源: 题型:
查看答案和解析>>【题目】在《几何原本》中记载着这样的题目:如果同一条线段被两个分点先后分成相等和不相等的线段,以得到的各线段为边作正方形,那么不相等的两个正方形的面积之和等于原线段一半上的正方形与两个分点之间一段上正方形的面积之和的两倍.王老师带领学生在阅读的基础上画出的部分图形如图,已知线段
 ,点
,点 为线段
为线段 的中点,点
的中点,点 为线段
为线段 上任意一点(
上任意一点( 不与
不与 重合),分别以
重合),分别以 和
和 为边在
为边在 的下方作正方形
的下方作正方形 和正方形
和正方形 ,以
,以 和
和 为边在线段下方作正方形
为边在线段下方作正方形 和正方形
和正方形 ,则正方形
,则正方形 与正方形
与正方形 的面积之和等于正方形
的面积之和等于正方形 和正方形
和正方形 面积之和的两倍.
面积之和的两倍.(1)请你画出正方形
 和正方形
和正方形 (不必尺规作图);
(不必尺规作图);(2)设
 ,
, ,根据题意写出关于
,根据题意写出关于 的等式并证明.
的等式并证明.
相关试题

