【题目】如图,ABCD中,M、N是BD的三等分点,连接CM并延长交AB于点E,连接EN并延长交CD于点F,以下结论:
①E为AB的中点;
②FC=4DF;
③S△ECF= ![]() ;
;
④当CE⊥BD时,△DFN是等腰三角形.
其中一定正确的是 . 
参考答案:
【答案】①③④
【解析】解:∵M、N是BD的三等分点,
∴DN=NM=BM,
∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,
∴△BEM∽△CDM,
∴ ![]() ,
,
∴BE= ![]() CD,
CD,
∴BE= ![]() AB,故①正确;
AB,故①正确;
∵AB∥CD,
∴△DFN∽△BEN,
∴ ![]() =
= ![]() ,
,
∴DF= ![]() BE,
BE,
∴DF= ![]() AB=
AB= ![]() CD,
CD,
∴CF=3DF,故②错误;
∵BM=MN,CM=2EM,
∴S△BEM=S△EMN= ![]() S△CBE,
S△CBE,
∵BE= ![]() CD,CF=
CD,CF= ![]() CD,
CD,
∴ ![]() =
= ![]() ,
,
∴S△EFC= ![]() S△CBE=
S△CBE= ![]() S△MNE,
S△MNE,
∴S△ECF= ![]() ,故③正确;
,故③正确;
∵BM=NM,EM⊥BD,
∴EB=EN,
∴∠ENB=∠EBN,
∵CD∥AB,
∴∠ABN=∠CDB,
∵∠DNF=∠BNE,
∴∠CDN=∠DNF,
∴△DFN是等腰三角形,故④正确;
所以答案是:①③④.
【考点精析】掌握平行四边形的性质和相似三角形的判定与性质是解答本题的根本,需要知道平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为支援雅安灾区,某学校计划用“义捐义卖”活动中筹集的部分资金用于购买A,B两种型号的学习用品共1000件,已知A型学习用品的单价为20元,B型学习用品的单价为30元.
(1)若购买这批学习用品用了26000元,则购买A,B两种学习用品各多少件?
(2)若购买这批学习用品的钱不超过28000元,则最多购买B型学习用品多少件?
-
科目: 来源: 题型:
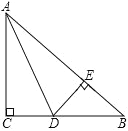
查看答案和解析>>【题目】如图,在
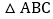 中,
中,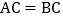 ,
,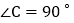 ,AD是
,AD是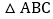 的角平分线,
的角平分线,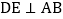 ,垂足为E.
,垂足为E.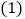 求证:
求证: ;
; 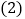 已知
已知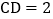 ,求AC的长;
,求AC的长; 求证:
求证: .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】从﹣3,﹣2,﹣1,0,1,2,3这七个数中随机抽取一个数记为a,则a的值是不等式组
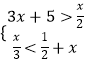 的解,但不是方程x2﹣3x+2=0的实数解的概率为 .
的解,但不是方程x2﹣3x+2=0的实数解的概率为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】某学习小组在探究三角形全等时,发现了下面这种典型的基本图形:
 如图1,已知:在
如图1,已知:在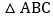 中,
中, ,
,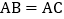 ,直线m经过点A,
,直线m经过点A, 直线m,
直线m,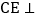 直线m,垂足分别为点D、
直线m,垂足分别为点D、 试猜想DE、BD、CE有怎样的数量关系,请直接写出;
试猜想DE、BD、CE有怎样的数量关系,请直接写出; 组员小颖想,如果三个角不是直角,那结论是否会成立呢?如图2,将
组员小颖想,如果三个角不是直角,那结论是否会成立呢?如图2,将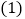 中的条件改为:在
中的条件改为:在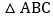 中,
中,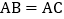 ,D、A、E三点都在直线m上,并且有
,D、A、E三点都在直线m上,并且有 其中
其中 为任意锐角或钝角
为任意锐角或钝角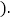 如果成立,请你给出证明;若不成立,请说明理由.
如果成立,请你给出证明;若不成立,请说明理由. 数学老师赞赏了他们的探索精神,并鼓励他们运用这个知识来解决问题:
数学老师赞赏了他们的探索精神,并鼓励他们运用这个知识来解决问题:如图3,F是
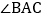 角平分线上的一点,且
角平分线上的一点,且 和
和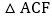 均为等边三角形,D、E分别是直线m上A点左右两侧的动点
均为等边三角形,D、E分别是直线m上A点左右两侧的动点 、E、A互不重合
、E、A互不重合 ,在运动过程中线段DE的长度始终为n,连接BD、CE,若
,在运动过程中线段DE的长度始终为n,连接BD、CE,若 ,试判断
,试判断 的形状,并说明理由.
的形状,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:在直角梯形ABCD中,AD∥BC,∠C=90°,AB=AD=25,BC=32.连接BD,AE⊥BD垂足为E.

(1)求证:△ABE∽△DBC;
(2)求线段AE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,反比例函数y=
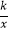 (x>0)的图象经过点A(1,2)和点B(m,n)(m>1),过点B作y轴的垂线,垂足为C.
(x>0)的图象经过点A(1,2)和点B(m,n)(m>1),过点B作y轴的垂线,垂足为C.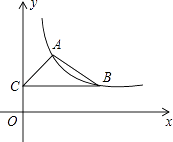
(1)求该反比例函数解析式;
(2)当△ABC面积为2时,求点B的坐标.
(3)P为线段AB上一动点(P不与A、B重合),在(2)的情况下,直线y=ax﹣1与线段AB交于点P,直接写出a的取值范围.
相关试题

