【题目】在计算![]() 的过程中,三位同学给出了不同的方法:
的过程中,三位同学给出了不同的方法:
甲同学的解法:原式=![]() ;
;
乙同学的解法:原式=![]() =1;
=1;
丙同学的解法:原式=(x+3)(x﹣2)+2﹣x=x2+x﹣6+2﹣x=x2﹣4.
(1)请你判断一下, 同学的解法从第一步开始就是错误的, 同学的解法是完全正确的.
(2)乙同学说:“我发现无论x取何值,计算的结果都是1”.请你评价一下乙同学的话是否合理,并简要说明理由.
参考答案:
【答案】(1)丙,乙;(2)不合理,理由见解析.
【解析】试题分析:(1)根据分式的加减法,由分解因式和同分母的分式加减,可知甲第2步去括号时没变号;乙正确;丙第一步的计算漏掉了分母,由此可知答案;
(2)根据乙的正确化简结果可知最终结果与x值无关,但是要注意所选取的x不能使分式无意义.
试题解析:(1)丙同学的解法从第一步开始就是错误的,乙同学的解法是完全正确的;
故答案为:丙,乙;
(2)不合理,
理由:∵当x≠±2时,![]() =
=![]() =1,
=1,
∴乙同学的话不合理,
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD的对角线AC、BD相交于点O,∠AOB=120°,CE∥BD,DE∥AC,若AD=4,则四边形CODE的周长 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,规定把一个点先绕原点逆时针旋转45°,再作出它关于原点的对称点称为一次变换,已知点A的坐标为(﹣2,0),把点A经过连续2014次这样的变换得到的点A2014的坐标是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点D,E分别是
 的边BC上两点,请你在下列三个式子
的边BC上两点,请你在下列三个式子 ,
, ,
, 中,选两个作为条件,余下的一个作为结论,编写一个说理题,并进行解答.
中,选两个作为条件,余下的一个作为结论,编写一个说理题,并进行解答.如图,已知点D,E分别是
 的边BC上两点______,______,那么______吗?为什么?
的边BC上两点______,______,那么______吗?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在平面直角坐标系中,
 的三个顶点坐标分别是
的三个顶点坐标分别是 ,
, ,
, ,其中
,其中 ,点C关于x轴的对称点为
,点C关于x轴的对称点为 ,
, 是等腰直角三角形.
是等腰直角三角形. 的值等于______;
的值等于______; 请直接写出
请直接写出
 把点A沿直线
把点A沿直线 翻折,落在点
翻折,落在点 的位置,如果点D在第一象限,
的位置,如果点D在第一象限, 是以
是以 为腰的等腰直角三角形,那么点D的坐标为______;
为腰的等腰直角三角形,那么点D的坐标为______; 请直接写出
请直接写出
 求四边形
求四边形 的面积.
的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为培养学生养成良好的“爱读书,读好书,好读书”的习惯,我市某中学举办了“汉字听写大赛”,准备为获奖同学颁奖.在购买奖品时发现,一个书包和一本词典会花去48元,用124元恰好可以购买3个书包和2本词典.
(1)每个书包和每本词典的价格各是多少元?
(2)学校计划总费用不超过900元,为获胜的40名同学颁发奖品(每人一个书包或一本词典),求最多可以购买多少个书包?
-
科目: 来源: 题型:
查看答案和解析>>【题目】投掷一枚质地均匀的正方体骰子.
(1)下列说法中正确的有 . (填序号)
①向上一面点数为1点和3点的可能性一样大;
②投掷6次,向上一面点数为1点的一定会出现1次;
③连续投掷2次,向上一面的点数之和不可能等于13.
(2)如果小明连续投掷了10次,其中有3次出现向上一面点数为6点,这时小明说:投掷正方体骰子,向上一面点数为6点的概率是
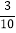 . 你同意他的说法吗?说说你的理由.
. 你同意他的说法吗?说说你的理由.(3)为了估计投掷正方体骰子出现6点朝上的概率,小亮采用转盘来代替骰子做实验.下图是一个可以自由转动的转盘,请你将转盘分为2个扇形区域,分别涂上红、白两种颜色,使得转动转盘,当转盘停止转动后,指针落在红色区域的概率与投掷正方体骰子出现6点朝上的概率相同.(友情提醒:在转盘上用文字注明颜色和扇形圆心角的度数.)
相关试题

