【题目】投掷一枚质地均匀的正方体骰子.
(1)下列说法中正确的有 . (填序号)
①向上一面点数为1点和3点的可能性一样大;
②投掷6次,向上一面点数为1点的一定会出现1次;
③连续投掷2次,向上一面的点数之和不可能等于13.
(2)如果小明连续投掷了10次,其中有3次出现向上一面点数为6点,这时小明说:投掷正方体骰子,向上一面点数为6点的概率是![]() . 你同意他的说法吗?说说你的理由.
. 你同意他的说法吗?说说你的理由.
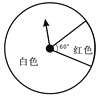
(3)为了估计投掷正方体骰子出现6点朝上的概率,小亮采用转盘来代替骰子做实验.下图是一个可以自由转动的转盘,请你将转盘分为2个扇形区域,分别涂上红、白两种颜色,使得转动转盘,当转盘停止转动后,指针落在红色区域的概率与投掷正方体骰子出现6点朝上的概率相同.(友情提醒:在转盘上用文字注明颜色和扇形圆心角的度数.)
参考答案:
【答案】(1) ①③;(2)见解析;(3)答案不唯一.
【解析】试题分析:(1)根据可能性大小来判定;
(2)![]() 是小明投掷正方体骰子,向上一面点数为6点的频率,不是概率.
是小明投掷正方体骰子,向上一面点数为6点的频率,不是概率.
(3)红色区域概率是![]() .
.
试题解析:(1) ①③
(2)![]() 是小明投掷正方体骰子,向上一面点数为6点的频率,不是概率.
是小明投掷正方体骰子,向上一面点数为6点的频率,不是概率.
一般地,在一定条件下大量重复同一试验时,随机事件发生的频率会在某个常数附近摆动.
只有当试验次数很大时,才能以事件发生的频率作为概率的估计值.
(3)本题答案不唯一,下列解法供参考
-
科目: 来源: 题型:
查看答案和解析>>【题目】在计算
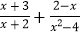 的过程中,三位同学给出了不同的方法:
的过程中,三位同学给出了不同的方法:甲同学的解法:原式=
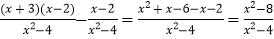 ;
;乙同学的解法:原式=
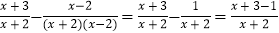 =1;
=1;丙同学的解法:原式=(x+3)(x﹣2)+2﹣x=x2+x﹣6+2﹣x=x2﹣4.
(1)请你判断一下, 同学的解法从第一步开始就是错误的, 同学的解法是完全正确的.
(2)乙同学说:“我发现无论x取何值,计算的结果都是1”.请你评价一下乙同学的话是否合理,并简要说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在平面直角坐标系中,
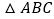 的三个顶点坐标分别是
的三个顶点坐标分别是 ,
, ,
, ,其中
,其中 ,点C关于x轴的对称点为
,点C关于x轴的对称点为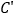 ,
, 是等腰直角三角形.
是等腰直角三角形. 的值等于______;
的值等于______; 请直接写出
请直接写出
 把点A沿直线
把点A沿直线 翻折,落在点
翻折,落在点 的位置,如果点D在第一象限,
的位置,如果点D在第一象限, 是以
是以 为腰的等腰直角三角形,那么点D的坐标为______;
为腰的等腰直角三角形,那么点D的坐标为______; 请直接写出
请直接写出
 求四边形
求四边形 的面积.
的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为培养学生养成良好的“爱读书,读好书,好读书”的习惯,我市某中学举办了“汉字听写大赛”,准备为获奖同学颁奖.在购买奖品时发现,一个书包和一本词典会花去48元,用124元恰好可以购买3个书包和2本词典.
(1)每个书包和每本词典的价格各是多少元?
(2)学校计划总费用不超过900元,为获胜的40名同学颁发奖品(每人一个书包或一本词典),求最多可以购买多少个书包?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司研发1000件新产品,需要精加工后才能投放市场.现在甲、乙两个工厂加工这批产品,已知甲工厂单独加工完成这批产品比乙工厂单独加工完成这批产品多用10天,而乙工厂每天加工的件数是甲工厂每天加工件数的1.25倍,公司需付甲工厂加工费用每天100元,乙工厂加工费用每天125元.
(1)甲、乙两个工厂每天各能加工多少件新产品?
(2)两个工厂同时合作完成这批产品,共付加工费多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论:①a+b+c<0;②a﹣b+c<0;③b+2a<0;④abc>0,其中正确的是(填编号)
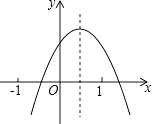
-
科目: 来源: 题型:
查看答案和解析>>【题目】小龙在学校组织的社会调查活动中负责了解他所居住的小区450户居民的家庭收入情况、他从中随机调查了40户居民家庭收入情况(收入取整数,单位:元),并绘制了如下的频数分布表和频数分布直方图:
分组
频数
百分比
600≤x<800
2
5%
800≤x<1000
6
15%
1000≤x<1200
45%
9
22.5%
1600≤x<1800
2
合计
40
100%
根据以上提供的信息,解答下列问题:
(1)补全频数分布表;
(2)补全频数分布直方图;

(3)请你估计该居民小区家庭属于中等收入(大于1000不足1600元)的大约有多少户?
相关试题

