【题目】如图,在平行四边形ABCD中,∠C=120°,AD=4,AB=2,点H、G分别是边CD、BC上的动点.连接AH、HG,点E为AH的中点,点F为GH的中点,连接EF则EF的最大值与最小值的差为__________.

参考答案:
【答案】![]()
【解析】
取AD的中点M,连接CM、AG、AC,作AN⊥BC于N;再证明∠ACD=90°,求出AC=2![]() 、AN=
、AN=![]() ;然后由三角形中位线定理,可得EF=
;然后由三角形中位线定理,可得EF=![]() AG,最后求出AG的最大值和最小值即可.
AG,最后求出AG的最大值和最小值即可.
解:如图:取AD的中点M,连接CM、AG、AC,作AN⊥BC于N

∵四边形ABCD是平行四边形,∠BCD= 120°
∴∠D=180°-∠BCD=60°,AB=CD=2
∴AM=DM=DC=2
∴△CDM是等边三角形
∴∠DMC=∠MCD=60°,AM=MC
∴∠MAC=∠MCA=30°
∴∠ACD=90°
∴AC=2![]()
在Rt△ACN中,AC=2![]() ,∠ACN=∠DAC=30°
,∠ACN=∠DAC=30°
∴AN=![]() AC=
AC=![]()
∵AE=EH,GF=FH
∴EF=![]() AG
AG
∴AG的最大值为AC的长,最小值为AN的长
∵AG的最大值为2![]() ,最小值为
,最小值为![]()
∴EF的最大值为![]() ,最小值为
,最小值为![]()
∴EF的最大值与最小值的差为![]() -
-![]() =
=![]() .
.
故答案为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于一个两位数,十位数字是
 ,个位数字是
,个位数字是 ,总有
,总有 ,我们把十位上的数与个位上的数的平方和叫做这个两位数的“平方和数”,把十位上的数与个位上的数的平方差叫做“平方差数”。例如,对两位数43来说,
,我们把十位上的数与个位上的数的平方和叫做这个两位数的“平方和数”,把十位上的数与个位上的数的平方差叫做“平方差数”。例如,对两位数43来说, ,
, ,所以25和7分别是43的“平方和数”与“平方差数”。
,所以25和7分别是43的“平方和数”与“平方差数”。(1)76的“平方和数”是_____________,“平万差数”是____________.
(2)5可以是___________的“平方差数”.
(3)若一个数的“平方和数”是10,“平方差数”是8,则这个数是______.
(4)若一个数的“平方和数”,与它的“平方差数”相等,那么这个数满足什么特征?为什么?(写出说明过程)
(5)若一个数的“平方差数”等子它十位上的数与个位上的数差的十倍,此时,我们把它叫做“凑整数”,请你写出两个这样的凑整数_____________,__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,等腰
 中,
中, ,
, ∥
∥ ,CD∥
,CD∥ ,点
,点 沿着
沿着 从
从 向
向 运动,同时点
运动,同时点 沿着
沿着 从
从 向
向 运动,
运动, 、
、 两点速度相同,当
两点速度相同,当 到达
到达 时,两点停止运动.
时,两点停止运动.
(1)图中有__________对全等三角形.请你找一对说明理由,写出过程.
(2)在
 、
、 运动过程中,图中阴影部分的面积是否发生变化?请说明理由.
运动过程中,图中阴影部分的面积是否发生变化?请说明理由.(3)当
 平分
平分 时,延长
时,延长 交
交 于
于 ,试说明
,试说明 .
.(4)在(3)的条件下,若
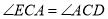 ,请问此时
,请问此时 点和
点和 点重合吗?为什么?
点重合吗?为什么? -
科目: 来源: 题型:
查看答案和解析>>【题目】在
 和
和 中,
中, .点
.点 在
在 上,BC、ED相交于点F,FE=FC,AB=DC,CF平分∠ACE.
上,BC、ED相交于点F,FE=FC,AB=DC,CF平分∠ACE.
(1)
 与
与 相等吗?请说明理由;
相等吗?请说明理由;(2)请说明
 是
是 中点的理由.
中点的理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,△ABC的位置如图所示(每个小方格都是边长为1个单位长度的正方形).
(1)将△ABC沿x轴方向向左平移6个单位,画出平移后得到的△A1B1C1;
(2)将△ABC绕着点A顺时针旋转90°,画出旋转后得到的△AB2C2,并直接写出点B2、C2的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的正方形网格中,每个小正方形的边长都为1个单位长度,三角形
 的顶点都在正方形网格的格点上,将三角形
的顶点都在正方形网格的格点上,将三角形 经过平移后得到三角形
经过平移后得到三角形 ,其中点
,其中点 是点
是点 的对应点.
的对应点.
(1)画出平移后得到的三角形
 ;
;(2)连接
 、
、 ,则线段
,则线段 、
、 的关系为______;
的关系为______;(3)四边形
 的面积为______(平方单位).
的面积为______(平方单位). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为1的正方形ABCD中,动点F,E分别以相同的速度从D,C两点同时出发向C和B运动(任何一个点到达即停止),过点P作PM∥CD交BC于M点,PN∥BC交CD于N点,连接MN,在运动过程中,则下列结论:①△ABE≌△BCF;②AE=BF;③AE⊥BF;④CF2=PEBF;⑤线段MN的最小值为
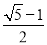 .其中正确的结论有( )
.其中正确的结论有( )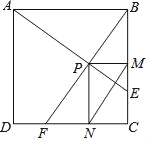
A. 2个 B. 3个 C. 4个 D. 5个
相关试题

