【题目】如图,以扇形 OAB 的顶点 O 为原点,半径 OB 所在的直线为 x 轴,建立平面直角坐标系,点 B 的坐标为(2,0),若抛物线 ![]() (n 为常数)与扇形 OAB 的边界总有两个公共点则 n 的取值范围是( )
(n 为常数)与扇形 OAB 的边界总有两个公共点则 n 的取值范围是( )

A.n>-4B.![]() C.
C.![]() D.
D.![]()
参考答案:
【答案】D
【解析】
根据∠AOB=45°求出直线OA的解析式,然后与抛物线解析式联立求出有一个公共点时的n值,即为一个交点时的最大值,再求出抛物线经过点B时的n的值,即为一个交点时的最小值,然后写出n的取值范围即可.
解:由图可知,∠AOB=45°,
∴直线OA的解析式为y=x,
联立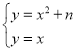 得:
得:![]() ,
,
![]() ,得
,得![]() 时,抛物线与OA有一个交点,
时,抛物线与OA有一个交点,
此交点的横坐标为![]() ,
,
∵点B的坐标为(2,0),
∴OA=2,
∴点A的横坐标与纵坐标均为:![]() ,
,
∴点A的坐标为(![]() ),
),
∴交点在线段AO上;
当抛物线经过点B(2,0)时,![]() ,解得n=-4,
,解得n=-4,
∴要使抛物线![]() 与扇形OAB的边界总有两个公共点,
与扇形OAB的边界总有两个公共点,
则实数n的取值范围是![]() ,
,
故选:D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图AC,BD是⊙O的两条直径,首位顺次连接A,B,C,D得到四边形ABCD,若AD=3,∠BAC=30°,则图中阴影部分的面积是______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,利用我们现在已经学过的圆和锐角三角函数的知识可知,半径 r 和圆心角θ及其所对的弦长 l之间的关系为
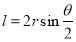 ,从而
,从而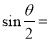
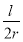 ,综合上述材料当
,综合上述材料当 时,
时,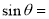 ______.
______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知一次函数 y=kx-2 的图象与 x 轴、y 轴分别交于 A,B 两点,与反比例函数
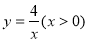 的图象交于点 C,且 AB=AC,则 k 的值为( )
的图象交于点 C,且 AB=AC,则 k 的值为( )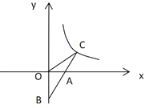
A.1B.2C.3D.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数
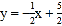 的图像与反比例函数
的图像与反比例函数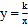 (k>0)的图像交于A,B两点,过点A做x轴的垂线,垂足为M,△AOM面积为1.
(k>0)的图像交于A,B两点,过点A做x轴的垂线,垂足为M,△AOM面积为1.(1)求反比例函数的解析式;
(2)在y轴上求一点P,使PA+PB的值最小,并求出其最小值和P点坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】随着通讯技术迅猛发展,人与人之间的沟通方式更多样、便捷.某校数学兴趣小组设计了“你最喜欢的沟通方式”调查问卷(每人必选且只选一种),在全校范围内随机调查了部分学生,将统计结果绘制了如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:
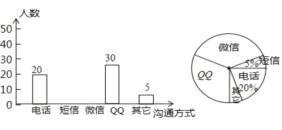
(1)在扇统计图中,表示“QQ”的扇形圆心角的度数为_____;根据这次统计数据了解到最受学生欢迎的沟通方式是______.
(2)将条形统计图补充完整;
(3)某天甲、乙两名同学都想从“微信”、“QQ”、“电话”三种沟通方式中选一种方式与对方联系,用列表或画树状图的方法求出甲、乙两名同学恰好选中同一种沟通方式的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,CD 为⊙O 的直径,弦 AB 交 CD 于点E,连接 BD、OB.

(1)求证:△AEC∽△DEB;
(2)若 CD⊥AB,AB=6,DE=1,求⊙O 的半径长.
相关试题

