【题目】如图,利用我们现在已经学过的圆和锐角三角函数的知识可知,半径 r 和圆心角θ及其所对的弦长 l之间的关系为![]() ,从而
,从而![]()
![]() ,综合上述材料当
,综合上述材料当![]() 时,
时,![]() ______.
______.

参考答案:
【答案】![]()
【解析】
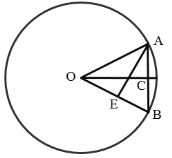
如图所示,∠AOB=θ,OA=r,AB=l,∠AOC=∠BOC=![]() ,根据
,根据![]() ,设AB=l=2a,OA =r=3a,根据等量代换得出∠BOC=∠BAE=
,设AB=l=2a,OA =r=3a,根据等量代换得出∠BOC=∠BAE=![]() ,求出BE,利用勾股定理求出AE,即可表达出
,求出BE,利用勾股定理求出AE,即可表达出![]() ,代入计算即可.
,代入计算即可.
解:如图所示,∠AOB=θ,OA=r,AB=l,∠AOC=∠BOC=![]() ,
,
∵AO=BO,
∴OC⊥AB,
∴![]() ,
,
∴设AB=l=2a,OA =r=3a,
过点A作AE⊥OB于点E,
∵∠B+∠BOC=90°,∠B+∠BAE=90°,
∴∠BOC=∠BAE=![]() ,
,
∴![]() ,即
,即![]() ,解得:
,解得:![]() ,
,
由勾股定理得:![]() ,
,
∴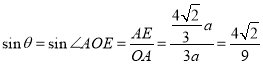 ,
,
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,E是BC的中点,连接DE、OE.
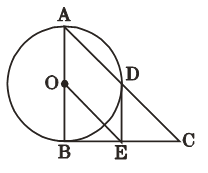
(1)判断DE与⊙O的位置关系并说明理由;
(2)求证:
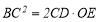
(3)若tanC=
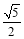 ,DE=2,求AD的长.
,DE=2,求AD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣x2+2mx+m+2的图象与x轴交于A(﹣1,0),B两点,在x轴上方且平行于x轴的直线EF与抛物线交于E,F两点,E在F的左侧,过E,F分别作x轴的垂线,垂足是M,N.
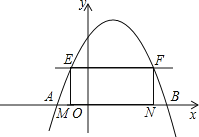
(1)求m的值及抛物线的顶点坐标;
(2)设BN=t,矩形EMNF的周长为C,求C与t的函数表达式;
(3)当矩形EMNF的周长为10时,将△ENM沿EN翻折,点M落在坐标平面内的点记为M',试判断点M'是否在抛物线上?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图AC,BD是⊙O的两条直径,首位顺次连接A,B,C,D得到四边形ABCD,若AD=3,∠BAC=30°,则图中阴影部分的面积是______.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知一次函数 y=kx-2 的图象与 x 轴、y 轴分别交于 A,B 两点,与反比例函数
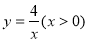 的图象交于点 C,且 AB=AC,则 k 的值为( )
的图象交于点 C,且 AB=AC,则 k 的值为( )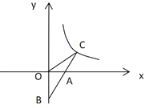
A.1B.2C.3D.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以扇形 OAB 的顶点 O 为原点,半径 OB 所在的直线为 x 轴,建立平面直角坐标系,点 B 的坐标为(2,0),若抛物线
 (n 为常数)与扇形 OAB 的边界总有两个公共点则 n 的取值范围是( )
(n 为常数)与扇形 OAB 的边界总有两个公共点则 n 的取值范围是( )
A.n>-4B.
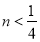 C.
C.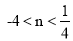 D.
D.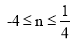
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数
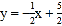 的图像与反比例函数
的图像与反比例函数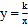 (k>0)的图像交于A,B两点,过点A做x轴的垂线,垂足为M,△AOM面积为1.
(k>0)的图像交于A,B两点,过点A做x轴的垂线,垂足为M,△AOM面积为1.(1)求反比例函数的解析式;
(2)在y轴上求一点P,使PA+PB的值最小,并求出其最小值和P点坐标.

相关试题

