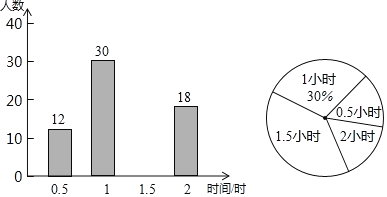
【题目】2019年8月,第18届世界警察和消防员运动会在成都举行.我们在体育馆随机调查了部分市民当天的观赛时间,并用得到的数据绘制了如下不完整的统计图,根据图中信息完成下列问题:
(1)将条形统计图补充完整;
(2)求抽查的市民观赛时间的众数、中位数;
(3)求所有被调查市民的平均观赛时间.
参考答案:
【答案】(1)答案见解析;(2)众数是1.5小时,中位数是1.5小时;(3)1.32小时.
【解析】
(1)根据观赛时间为1小时的人数和所占的百分比可以求得本次调查的人数,从而可以得到观赛时间为1.5小时的人数,进而可以将条形统计图补充完整;
(2)根据(1)中条形统计图中的数据可以得到抽查的市民观赛时间的众数、中位数;
(3)根据条形统计图中的数据可以计算出所有被调查市民的平均观赛时间.
(1)本次调查的人数为:30÷30%=100,
观赛时间为1.5小时的有:100﹣12﹣30﹣18=40(人),
补全的条形统计图如右图所示;
(2)由(1)中的条形统计图可知,
抽查的市民观赛时间的众数、中位数分别是1.5小时、1.5小时;
(3)![]() 1.32(小时),
1.32(小时),
答:所有被调查市民的平均观赛时间是1.32小时.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,一次函数y
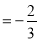 x+4的图象与x轴和y轴分别交于A、B两点.动点P从点A出发,在线段AO上以每秒1个单位长度的速度向点O作匀速运动,到达点O即停止运动.其中A、Q两点关于点P对称,以线段PQ为边向上作正方形PQMN.设运动时间为秒.如图①.
x+4的图象与x轴和y轴分别交于A、B两点.动点P从点A出发,在线段AO上以每秒1个单位长度的速度向点O作匀速运动,到达点O即停止运动.其中A、Q两点关于点P对称,以线段PQ为边向上作正方形PQMN.设运动时间为秒.如图①.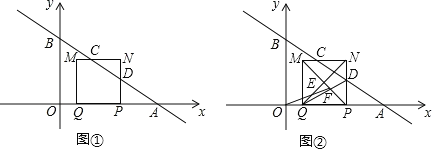
(1)当t=2秒时,OQ的长度为 ;
(2)设MN、PN分别与直线y
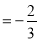 x+4交于点C、D,求证:MC=NC;
x+4交于点C、D,求证:MC=NC;(3)在运动过程中,设正方形PQMN的对角线交于点E,MP与QD交于点F,如图2,求OF+EN的最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,AC=BC,斜边AB=2,O是AB的中点,以O为圆心,线段OC的长为半径画圆心角为90°的扇形OEF,弧EF经过点C,则图中阴影部分的面积为________.
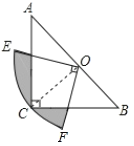
-
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△POQ中,OP=OQ=4,M是PQ中点,把一三角尺的直角顶点放在点M处,以M为旋转中心,旋转三角尺,三角尺的两直角边与△POQ的两直角边分别交于点A、B.求证:MA=MB;

-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题10分)如图,直线y=x+m和抛物线y=
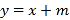 +bx+c都经过点A(1,0),
+bx+c都经过点A(1,0),B(3,2).
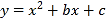
(1)求m的值和抛物线的解析式;
(2)求不等式x2+bx+c>x+m的解集.(直接写出答案)
-
科目: 来源: 题型:
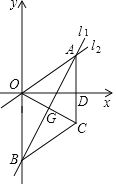
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线l:y
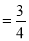 x与直线l:y=kx+b相交于点A(a,3),直线交l交y轴于点B(0,﹣5).
x与直线l:y=kx+b相交于点A(a,3),直线交l交y轴于点B(0,﹣5).(1)求直线l的解析式;
(2)将△OAB沿直线l翻折得到△CAB(其中点O的对应点为点C),求证:AC∥OB;
(3)在直线BC下方以BC为边作等腰直角三角形BCP,直接写出点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知三条线段的长分别为
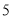 厘米,
厘米, 厘米,
厘米,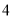 厘米,以其中两条为对角线,另一条为一边,可以画出______个平行四边形.
厘米,以其中两条为对角线,另一条为一边,可以画出______个平行四边形.
相关试题

