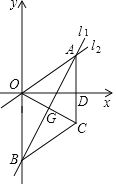
【题目】如图,在平面直角坐标系中,直线l:y![]() x与直线l:y=kx+b相交于点A(a,3),直线交l交y轴于点B(0,﹣5).
x与直线l:y=kx+b相交于点A(a,3),直线交l交y轴于点B(0,﹣5).
(1)求直线l的解析式;
(2)将△OAB沿直线l翻折得到△CAB(其中点O的对应点为点C),求证:AC∥OB;
(3)在直线BC下方以BC为边作等腰直角三角形BCP,直接写出点P的坐标.
参考答案:
【答案】(1)直线l的解析式为y=2x﹣5;(2)证明见解析;(3)P1(0,﹣9),P2(7,﹣6),P3(![]() ,
,![]() ).
).
【解析】
(1)解方程得到A(4,3),待定系数法即可得到结论;
(2)根据勾股定理得到OA=5,根据等腰三角形的性质得到∠OAB=∠OBA,根据折叠的性质得到∠OAB=∠CAB,于是得到结论;
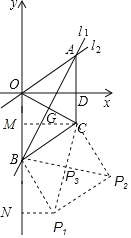
(3)如图,过C作CM⊥OB于M,求得CM=OD=4,得到C(4,-2),过P1作P1N⊥y轴于N,根据全等三角形的判定和性质定理即可得到结论.
(1)∵直线l:y![]() x与直线l:y=kx+b相交于点A(a,3),∴A(4,3).
x与直线l:y=kx+b相交于点A(a,3),∴A(4,3).
∵直线交l交y轴于点B(0,﹣5),∴y=kx﹣5,
把A(4,3)代入得:3=4k﹣5,
∴k=2,
∴直线l的解析式为y=2x﹣5;
(2)∵OA![]() 5,
5,
∴OA=OB,∴∠OAB=∠OBA.
∵将△OAB沿直线l翻折得到△CAB,
∴∠OAB=∠CAB,∴∠OBA=∠CAB,
∴AC∥OB;
(3)如图,过C作CM⊥OB于M,
则CM=OD=4.
∵BC=OB=5,∴BM=3,
∴OB=2,∴C(4,﹣2),
过P1作P1N⊥y轴于N.
∵△BCP是等腰直角三角形,
∴∠CBP1=90°,∴∠MCB=∠NBP1.
∵BC=BP1,
∴△BCM≌△P1BN(AAS),
∴BN=CM=4,∴P1(0,﹣9);
同理可得:P2(7,﹣6),P3(![]() ,
,![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△POQ中,OP=OQ=4,M是PQ中点,把一三角尺的直角顶点放在点M处,以M为旋转中心,旋转三角尺,三角尺的两直角边与△POQ的两直角边分别交于点A、B.求证:MA=MB;

-
科目: 来源: 题型:
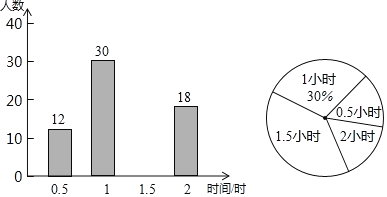
查看答案和解析>>【题目】2019年8月,第18届世界警察和消防员运动会在成都举行.我们在体育馆随机调查了部分市民当天的观赛时间,并用得到的数据绘制了如下不完整的统计图,根据图中信息完成下列问题:
(1)将条形统计图补充完整;
(2)求抽查的市民观赛时间的众数、中位数;
(3)求所有被调查市民的平均观赛时间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题10分)如图,直线y=x+m和抛物线y=
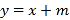 +bx+c都经过点A(1,0),
+bx+c都经过点A(1,0),B(3,2).
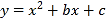
(1)求m的值和抛物线的解析式;
(2)求不等式x2+bx+c>x+m的解集.(直接写出答案)
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知三条线段的长分别为
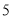 厘米,
厘米, 厘米,
厘米,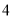 厘米,以其中两条为对角线,另一条为一边,可以画出______个平行四边形.
厘米,以其中两条为对角线,另一条为一边,可以画出______个平行四边形. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2 - 2(1-m)x+m2的两实数根为x1,x2.
(1)求m的取值范围;
(2)设
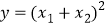 ,当m为何值时,y有最小值,求y的最小值.
,当m为何值时,y有最小值,求y的最小值. -
科目: 来源: 题型:
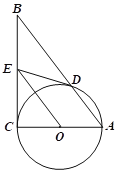
查看答案和解析>>【题目】如图在RtΔABC中,∠C=90°,以AC为直径作⊙O,交AB于D,过O作OE∥AB,交BC于E.
(1)求证:ED是⊙O的切线;
(2)如果⊙O的半径为1.5,ED=2,求AB的长.
(3)在(2)的条件下,求△ADO的面积.
相关试题

