搜索
【题目】某校初二年级四个班的同学外出植树一天，已知每小时5个女生种3棵树，3个男生种5棵树，各班人数如图所示，则植树最多的是初二几班．
参考答案：
【答案】三班．
【解析】
由条形统计图得到各班的男女学生人数，由每班男、女生种树的速度相同，所以每班人数减去相同的女生数和男生数，计算剩下的男生与女生种的数的数量即可得到答案．
解：由图可知
一班 | 二班 | 三班 | 四班 | |
女生数(人) | 22 | 18 | 13 | 15 |
男生数(人) | 18 | 20 | 22 | 21 |
因为每班男、女生种树的速度相同，所以每班人数减去相同的女生数和男生数，比较结果不变，每个班减去13个女生和18个男生，一班余下女生9人，可植树
×9＝5
(棵)．二班余下女生5人和男生2人，可植树×5＋
×2＝6
(棵)．三班余下男生4人，可植树×4＝6
(棵)．四班余下女生2人和男生3人，可植树×2＋×3＝6
(棵)．所以种树最多的班级是三班．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在我们学习过的数学教科书中，有一个数学活动，其具体操作过程是：
第一步：对折矩形纸片
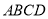，使
与
重合，得到折痕
，把纸片展开（如图①）；第二步：再一次折叠纸片，使点
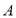落在上，并使折痕经过点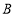
，得到折痕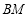
，同时得到线段
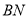（如图②）．如图②所示建立平面直角坐标系，请解答以下问题：
（Ⅰ）设直线
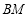的解析式为
，求
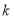的值；（Ⅱ）若
的延长线与矩形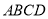的边交于点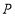
，设矩形的边
，
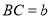；（i）若
，
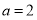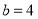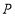，求点的坐标；（ii）请直接写出
、
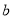应该满足的条件．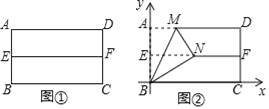
-
科目： 来源： 题型：
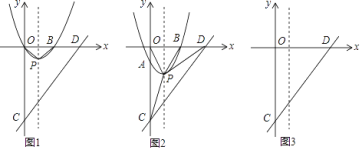
查看答案和解析>>【题目】如图，平面直角坐标系中，抛物线y=x2﹣2x与x轴交于O、B两点，顶点为P，连接OP、BP，直线y=x﹣4与y轴交于点C，与x轴交于点D．
（1）写出点B坐标；判断△OBP的形状；
（2）将抛物线沿对称轴平移m个单位长度，平移的过程中交y轴于点A，分别连接CP、DP；
（i）若抛物线向下平移m个单位长度，当S△PCD=
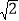S△POC时，求平移后的抛物线的顶点坐标；（ii）在平移过程中，试探究S△PCD和S△POD之间的数量关系，直接写出它们之间的数量关系及对应的m的取值范围．
-
科目： 来源： 题型：
查看答案和解析>>【题目】在直角坐标系中，O为坐标原点，A（1，1），在x轴上确定点P，使△AOP为等腰三角形，则符合条件的点P的个数共有（ ）
A.4个B.3个C.2个D.1个
-
科目： 来源： 题型：
查看答案和解析>>【题目】声音在空气中传播的速度y（米/秒）是气温x (摄氏度)的一次函数，下表列出了一组不同气温时的音速．
气温x/摄氏度
0
5
10
15
20
音速y/(米/秒)
331
334
337
340
343
（1）求y 与 x之间的函数关系式
（2）气温x=22(摄氏度)时，某人看到烟花燃放5秒后才听到声响，那么此人与燃放的烟花所在地相距多远？
-
科目： 来源： 题型：
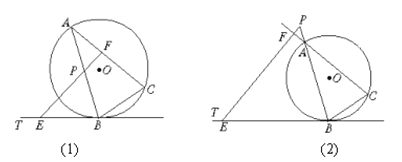
查看答案和解析>>【题目】已知：△ABC是⊙O的内接三角形，BT为⊙O的切线，B为切点，P为直线AB上一点，过P作BC的平行线交直线BT于点E，交直线AC于点F．
(1)如图 (1)所示，当P在线段AB上时，求证：PA·PB＝PE·PF；
(2)如图 (2)所示，当P为线段BA延长线上一点时，第(1)题的结论还成立吗？如果成立，请给出证明；如果不成立，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】先仔细阅读下列材料，然后回答问题：
如果a＞0，b＞0，那么(
-
)2≥0，即a＋b-2
≥0 得
≥，其中，当a＝b时取等号，我们把称为a、b的算术平均数， 称为a、b的几何平均数．如果a＞0，b＞0，c＞0，同样可以得到
≥
，其中，当a＝b＝c时取等号于是就有定理：几个正数的算术平均数不小于它们的几何平均数．请用上述定理解答问题：把边长为30 cm的正方形纸片的4角各剪去一个小正方形，折成无盖纸盒(如图)(1)设剪去的小正方形边长为x cm，无盖纸盒的容积为V，求V与x的函数关系式及x的取值范围．
(2)当x为何值时，容积V有最大值，最大值是多少？
相关试题
