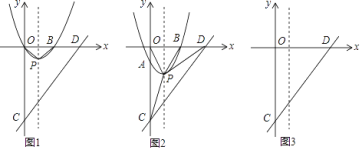
【题目】如图,平面直角坐标系中,抛物线y=x2﹣2x与x轴交于O、B两点,顶点为P,连接OP、BP,直线y=x﹣4与y轴交于点C,与x轴交于点D.
(1)写出点B坐标;判断△OBP的形状;
(2)将抛物线沿对称轴平移m个单位长度,平移的过程中交y轴于点A,分别连接CP、DP;
(i)若抛物线向下平移m个单位长度,当S△PCD= ![]() S△POC时,求平移后的抛物线的顶点坐标;
S△POC时,求平移后的抛物线的顶点坐标;
(ii)在平移过程中,试探究S△PCD和S△POD之间的数量关系,直接写出它们之间的数量关系及对应的m的取值范围.
参考答案:
【答案】(1)(2,0);等腰直角三角形;(2)(i)![]() 或
或![]() ;(ii)当m≥2时,S△POD﹣S△PCD=6;当﹣1≤m<2时,S△POD+S△PCD=6;当m<﹣1时,S△POD﹣S△PCD=6.
;(ii)当m≥2时,S△POD﹣S△PCD=6;当﹣1≤m<2时,S△POD+S△PCD=6;当m<﹣1时,S△POD﹣S△PCD=6.
【解析】
(1)根据自变量与函数值得对应关系,可得B点坐标,根据配方法,可得顶点坐标,根据勾股定理及勾股定理的逆定理,可得答案;
(2)根据自变量与函数值得对应关系,可得C,D,M点坐标,根据平移规律,可得P点坐标,根据平行于y轴的直线上两点间的距离较大的纵坐标减较小的纵坐标,可得PM的长,(i)根据面积的关系,可得关于m的方程,根据解方程,可得到顶点坐标;(ii)根据三角形的面积,可得答案.
(1)当y=0时,x2﹣2x=0,解得x=0(舍)或x=2,即B点坐标为(2,0),
∵抛物线y=x2﹣2x=(x﹣1)2﹣1,
∴P点坐标为(1,﹣1),由勾股定理,得
OP2=(2﹣1)2+12=2,
∴OP2+BP2=OB2 , OP=BP,
∴△OBP是等腰直角三角形,
(2)解:∵直线y=x﹣4与y轴交于点C,与x轴交于点D,
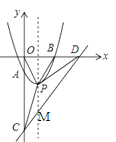
∴C(0,﹣4),D(4,0),当x=1时,y=﹣3,即M(1,﹣3),
抛物线向下平移m个单位长度,解析式为y=(x﹣1)2﹣(1+m),P(1,﹣1﹣m),
∴![]()
S△PCD=S△PMC+S△PMD= ![]() PM|xP﹣xC|=
PM|xP﹣xC|= ![]() |m﹣2|×4=2|m﹣2|,
|m﹣2|×4=2|m﹣2|,
(i)S△POC= ![]() AC|xP|=
AC|xP|= ![]() ×4×1=2,
×4×1=2,
∵S△PCD= ![]() S△POC,
S△POC,
∴S△PCD=2|m﹣2|=2![]() ,
,
解得m=2+ ![]() 或m=2﹣
或m=2﹣![]() ,
,
∴![]() 或
或![]() ;
;
(ii)![]()
①当m≥2时,S△PCD=2|m﹣2|=2m﹣4,S△POD=2|m+1|=2m+2,
∴S△POD﹣S△PCD=6
②当﹣1≤m<2时,S△PCD=2|m﹣2=4﹣2m,S△POD=2|m+1|=2m+2,
∴S△POD+S△PCD=6
③当m<﹣1时,S△PCD=2|m﹣2|=4﹣2m,S△POD=2|m+1|=2﹣2m,
∴S△POD﹣S△PCD=6,
综上所述:当m≥2时,S△POD﹣S△PCD=6;当﹣1≤m<2时,S△POD+S△PCD=6;当m<﹣1时,S△POD﹣S△PCD=6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(6分)株洲五桥主桥主孔为拱梁钢构组合体系(如图1),小明暑假旅游时,来到五桥观光,发现拱梁的路面部分有均匀排列着9根支柱,他回家上网查到了拱梁是抛物线,其跨度为20米,拱高(中柱)10米,于是他建立如图2的坐标系,发现可以将余下的8根支柱的高度都算出来了,请你求出中柱左边第二根支柱CD的高度.


-
科目: 来源: 题型:
查看答案和解析>>【题目】为了“创建文明城市,建设美丽家园”,我市某社区将辖区内的一块面积为1000m2的空地进行绿化,一部分种草,剩余部分栽花,设种草部分的面积为
 (m2),种草所需费用
(m2),种草所需费用 1(元)与
1(元)与 (m2)的函数关系式为
(m2)的函数关系式为 ,其图象如图所示:栽花所需费用
,其图象如图所示:栽花所需费用 2(元)与x(m2)的函数关系式为
2(元)与x(m2)的函数关系式为 2=﹣0.01
2=﹣0.01 2﹣20
2﹣20 +30000(0≤
+30000(0≤ ≤1000).
≤1000).
(1)请直接写出k1、k2和b的值;
(2)设这块1000m2空地的绿化总费用为W(元),请利用W与
 的函数关系式,求出绿化总费用W的最大值;
的函数关系式,求出绿化总费用W的最大值;(3)若种草部分的面积不少于700m2,栽花部分的面积不少于100m2,请求出绿化总费用W的最小值.
-
科目: 来源: 题型:
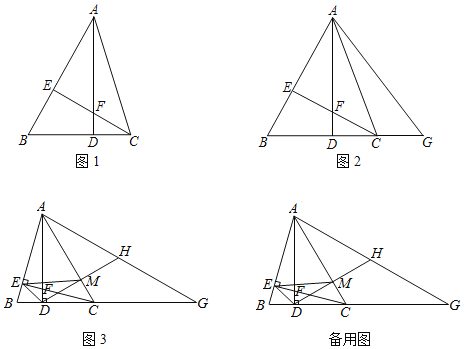
查看答案和解析>>【题目】如图1,在△ABC中,AD⊥BC于D,CE⊥AB于E,AD与CE交于点F,∠ACE=45°.
(1)求证:BE=EF;
(2)如图2,G在BC的延长线上,连接GA,若GA=GB,求证:AC平分∠DAG;
(3)如图3,在(2)的条件下,H为AG的中点,连接DH交AC于M,连接EM、ED,若S△EMC=4,∠BAD=15°,求AM的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,点A坐标为(2,0),点B在x轴负半轴上,C在y轴正半轴上,∠ACB=90°,∠ABC=30°.
(1)求点B坐标;
(2)如图2,点P从B出发,沿线段BC运动,点P运动速度为每秒2个单位长度,设运动时间为t秒,用含t的式子表示三角形△OBP的面积S;
(3)如图3,在(2)的条件下,点P出发的同时,点Q从O出发,在线段OC上运动,运动速度为每秒2个单位长度,一个点到达终点,另一个点也停止运动.连接PQ,以PQ为一边,在第二象限作等边△PQM,作ME⊥y轴于E,点D为PC中点,作DN⊥BC交y轴于N,若CE=BP,BC=4
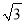 ,求N的坐标.
,求N的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AD平分
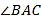 ,AB=AC,则此图中全等三角形有( )
,AB=AC,则此图中全等三角形有( )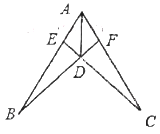
A.2对B.3对C.4对D.5对
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠AOB=20°,点P在OA边上.
(1)以点O为圆心,OP长为半径作
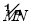 ,交OB于点C;
,交OB于点C;(2)分别以点P、C为圆心,PC长为半径作弧,交
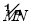 于点D、E;
于点D、E;(3)连接DE,分别交OC、OP于点F、G;
(4)连接DP.
根据以上作图过程及所作图形,下列结中正确的是_____.(填序号)
①OC垂直平分DP;②∠COD=∠COP;③DF=FG;④OD=DE.
相关试题

