搜索
【题目】在直角坐标系中，O为坐标原点，A（1，1），在x轴上确定点P，使△AOP为等腰三角形，则符合条件的点P的个数共有（ ）
A.4个B.3个C.2个D.1个
参考答案：
【答案】A
【解析】
有三种情况：当OA=OP时，以O为圆心，以OA为半径画弧交x轴于两点；当OA=AP时，以A为圆心，以OA为半径画弧交x轴于一点；当OP=AP时，根据线段垂直平分线的性质作OA的垂直平分线，交x轴于点P，综上即可得答案.
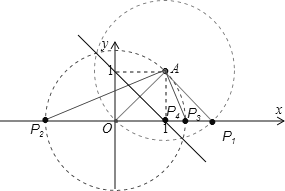
如图，当OA=OP时，以O为圆心，以OA为半径画弧交x轴于两点（P2、P3），
当OA=AP时，以A为圆心，以OA为半径画弧交x轴于一点（P1），
当OP=AP时，作OA的垂直平分线，交x轴于一点（P4）.
∴符合使△AOP为等腰三角形的点P有4个，
故选A.
-
科目： 来源： 题型：
查看答案和解析>>【题目】（本题满分8分）
如图，点E，F在BC上，BE＝CF，∠A＝∠D，∠B＝∠C，AF与DE交于点O．
(1)求证：AB＝DC；
(2)试判断△OEF的形状，并说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：如图①，在△ABC中，BC=AC，在△CDE中，CE=CD，现把两个三角形的C点重合，且使∠BCA=∠ECD，连接BE、AD.
(1)求证：BE=AD
(2)若将△ECD绕点C旋转至图②、③所示的情况时，其余条件不变，BE与AD还相等么？若相等，请给与证明；若不相等，请说明理由.
-
科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系
中，抛物线
与
轴的交点分别为
，
．
求证：抛物线总与轴有两个不同的交点；
若
，求此抛物线的解析式．
已知轴上两点
，
，若抛物线与线段
有交点，请写出
的取值范围． -
科目： 来源： 题型：
查看答案和解析>>【题目】悦达汽车4S店“十一”黄金周销售某种型号汽车，该型号汽车的进价为30万元/辆，若黄金周期间销售量超过5辆时，每多售出1辆，所有售出的汽车进价均降低0.1万元/辆．根据市场调查，黄金周期间销售量不会突破30台．已知该型号汽车的销售价为32万元/辆，悦达汽车4S店计划黄金周期间销售利润25万元，那么需售出多少辆汽车？（注：销售利润=销售价﹣进价）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，某幼儿园有一道长为
米的墙，计划用
米长的围栏利用一面墙如图围成一个矩形草坪
．设该矩形草坪
边的长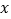为
米，面积为
平方米．
求出与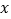的函数关系式并写出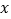的取值范围；
如果所围成的矩形草坪面积为
平方米，试求边的长；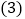
按题目的设计要求，________（填“能”或“不能”）围成面积为
平方米的矩形草坪．
-
科目： 来源： 题型：
查看答案和解析>>【题目】“2017年张学友演唱会”于6月3日在我市关山湖奥体中心举办，小张去离家2520米的奥体中心看演唱会，到奥体中心后，发现演唱会门票忘带了，此时离演唱会开始还有23分钟，于是他跑步回家，拿到票后立刻找到一辆“共享单车”原路赶回奥体中心，已知小张骑车的时间比跑步的时间少用了4分钟，且骑车的平均速度是跑步的平均速度的1.5倍．
（1）求小张跑步的平均速度；
（2）如果小张在家取票和寻找“共享单车”共用了5分钟，他能否在演唱会开始前赶到奥体中心？说明理由．
相关试题
