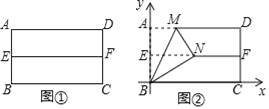
【题目】在我们学习过的数学教科书中,有一个数学活动,其具体操作过程是:
第一步:对折矩形纸片![]() ,使
,使![]() 与
与![]() 重合,得到折痕
重合,得到折痕![]() ,把纸片展开(如图①);
,把纸片展开(如图①);
第二步:再一次折叠纸片,使点![]() 落在
落在![]() 上,并使折痕经过点
上,并使折痕经过点![]() ,得到折痕
,得到折痕![]() ,同时得到线段
,同时得到线段![]() (如图②).
(如图②).
如图②所示建立平面直角坐标系,请解答以下问题:
(Ⅰ)设直线![]() 的解析式为
的解析式为![]() ,求
,求![]() 的值;
的值;
(Ⅱ)若![]() 的延长线与矩形
的延长线与矩形![]() 的边
的边![]() 交于点
交于点![]() ,设矩形的边
,设矩形的边![]() ,
,![]() ;
;
(i)若![]() ,
,![]() ,求
,求![]() 点的坐标;
点的坐标;
(ii)请直接写出![]() 、
、![]() 应该满足的条件.
应该满足的条件.
参考答案:
【答案】(Ⅰ)![]() ;(Ⅱ)(i)
;(Ⅱ)(i)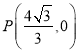 ;(ii)
;(ii)![]() .
.
【解析】
(Ⅰ)连接![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,由折叠的性质可证
,由折叠的性质可证![]() 为等边三角形,由
为等边三角形,由![]() 点的坐标可求得
点的坐标可求得![]() 的值;
的值;
(Ⅱ)(i)在![]() 中,由三角形的性质可求得
中,由三角形的性质可求得![]() 的长,则可求得
的长,则可求得![]() 的长,可求得
的长,可求得![]() 点坐标;
点坐标;
(ii)由题意可知![]() ,在
,在![]() 中,由三角函数的定义可用
中,由三角函数的定义可用![]() 表示出
表示出![]() ,则可得到
,则可得到![]() 、
、![]() 所满足的条件.
所满足的条件.
(Ⅰ)连接AN,延长MN交BC于点P,如图,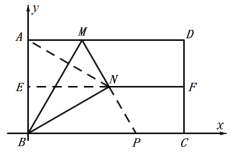
∴EF垂直平分AB,
∴AN=BN,
由折叠知AB=BN,
∴AN=AB=BN,
∴△ABN为等边三角形,
∴∠ABN=60°,
∴∠PBN=30°,
∵∠ABM=∠NBM=30°,
∴∠BNM=∠BAM=90°,
∴∠BPN=60°,∠MBP=∠MBN+∠PBN=60°,
∴∠BMP=60°,
∴∠MBP=∠BMP=∠BPM=60°,
∴△BMP是等边三角形,
∵点M在直线![]() 上,
上,
∴![]() ;
;
(Ⅱ)(i)由题意可知![]() ,
,
在![]() 中,
中,![]() ,
,
∴![]() ,解得
,解得![]() ,
,
∴![]() ,
,
∴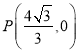 ;
;
(ii)由题意可知![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
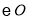 的直径
的直径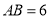 ,
,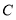 为圆周上一点,
为圆周上一点,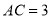 ,过点
,过点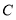 作
作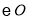 的切线
的切线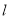 ,过点
,过点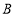 作
作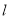 的垂线
的垂线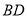 ,垂足为
,垂足为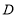 ,
,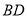 与
与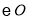 交于点
交于点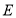 .
.(1)求
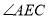 的度数;
的度数;(2)求证:四边形
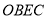 是菱形.
是菱形.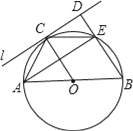
-
科目: 来源: 题型:
查看答案和解析>>【题目】图,小东在教学楼距地面9米高的窗口C处,测得正前方旗杆顶部A点的仰角为37°,旗杆底部B点的俯角为45°,升旗时,国旗上端悬挂在距地面2.25米处,若国旗随国歌声冉冉升起,并在国歌播放45秒结束时到达旗杆顶端,则国旗应以多少米/秒的速度匀速上升?(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了提高身体素质,有些人选择到专业的健身中心锻炼身体,某健身中心的消费方式如下:
普通消费:35元/次;
白金卡消费:购卡280元/张,凭卡免费消费10次再送2次;
钻石卡消费:购卡560元/张,凭卡每次消费不再收费.
以上消费卡使用年限均为一年,每位顾客只能购买一张卡,且只限本人使用.
(1)李叔叔每年去该健身中心健身6次,他应选择哪种消费方式更合算?
(2)设一年内去该健身中心健身x次(x为正整数),所需总费用为y元,请分别写出选择普通消费和白金卡消费的y与x的函数关系式;
(3)王阿姨每年去该健身中心健身至少18次,请通过计算帮助王阿姨选择最合算的消费方式.
-
科目: 来源: 题型:
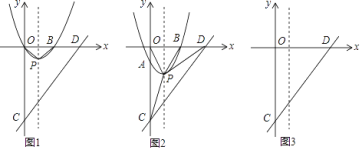
查看答案和解析>>【题目】如图,平面直角坐标系中,抛物线y=x2﹣2x与x轴交于O、B两点,顶点为P,连接OP、BP,直线y=x﹣4与y轴交于点C,与x轴交于点D.
(1)写出点B坐标;判断△OBP的形状;
(2)将抛物线沿对称轴平移m个单位长度,平移的过程中交y轴于点A,分别连接CP、DP;
(i)若抛物线向下平移m个单位长度,当S△PCD=
 S△POC时,求平移后的抛物线的顶点坐标;
S△POC时,求平移后的抛物线的顶点坐标;(ii)在平移过程中,试探究S△PCD和S△POD之间的数量关系,直接写出它们之间的数量关系及对应的m的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系中,O为坐标原点,A(1,1),在x轴上确定点P,使△AOP为等腰三角形,则符合条件的点P的个数共有( )
A.4个B.3个C.2个D.1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校初二年级四个班的同学外出植树一天,已知每小时5个女生种3棵树,3个男生种5棵树,各班人数如图所示,则植树最多的是初二几班.

相关试题

