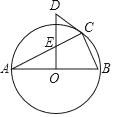
【题目】如图,△ABC内接于⊙O,且AB为⊙O的直径OD⊥AB,与AC交于点E,与过点C的⊙O切线交于点D.
(1)若AC=6,BC=3,求OE的长.
(2)试判断∠A与∠CDE的数量关系,并说明理由.
参考答案:
【答案】(1)证明见解析;(2)∠CDE=2∠A,理由见解析.
【解析】分析:(1)由勾股定理求AB,证明△AOE∽△ACB,根据相似三角形的对应线段成比例求OE;(2)连接OC,可知∠3=2∠A,只需用同角的余角证∠D=∠3即可.
详解:(1)∵AB为⊙O的直径,∴∠ACB=900,
在Rt△ABC中,由勾股定理得:AB=![]() =3
=3![]() ,
,
∴OA=![]() AB=
AB=![]() .
.
∵OD⊥AB,∴∠AOE=∠ACB=900,由∵∠A=∠A,∴△AOE∽△ACB,
∴![]() ,即
,即![]() ,解得:OE=
,解得:OE=![]() .
.
(2)∠CDE=2∠A,
理由如下:连接OC,如图所示:
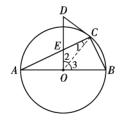
∵OA=OC,∴∠1=∠A,
∵CD是⊙O的切线,∴OC⊥CD,∴∠OCD=900,∴∠2+∠CDE=900,
∵OD⊥AB,∴∠2+∠3=900,∴∠3=∠CDE,∵∠3=∠A+∠1=2∠A,
∴∠CDE=2∠A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(10分)下面的图形是由边长为l的正方形按照某种规律排列而组成的.
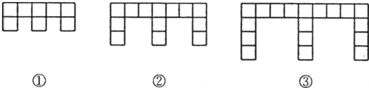
(1)观察图形,填写下表:
图形
①
②
③
正方形的个数
8
图形的周长
18
(2)推测第n个图形中,正方形的个数为 ,周长为 (都用含n的代数式表示).
(3)这些图形中,任意一个图形的周长y与它所含正方形个数x之间的关系可表示为y= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着科技的迅猛发展,人与人之间的沟通方式更多样、便捷某校数学兴趣小组设计了“你最喜欢的沟通方式”调查问卷(每人必选且只选一种),在全校范围内随机调查了部分学生,将统计结果绘制了如下两幅不完整的统计图,请结合图中所给的信息解答下列问题.
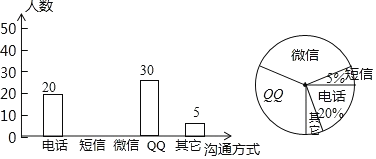
(1)这次统计共抽查了______名学生;在扇形统计图中,表示“QQ”的扇形圆心角的度数为________;
(2)将条形统计图补充完整;
(3)该校共有2500名学生,请估计该校最喜欢用“微信”进行沟通的学生有多少名?
(4)某天甲、乙两名同学都想从“微信”“QQ”“电话”三种沟通方式中选一种方式与对方联系,请用列表或画树状图的方法求出甲、乙两名同学恰好选择同一种沟通方式的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场将进货价为35元台灯以50元销售价售出,平均每月能售出500个,市场调研表明:当销售价每上涨1元时,其销售量就将减少10个
 若设每个台灯的销售价上涨a元.
若设每个台灯的销售价上涨a元. 试用含a的代数式填空:涨价后,每个台灯的销售价为______元,利润为______元,商场的台灯平均每月的销售量为______台
试用含a的代数式填空:涨价后,每个台灯的销售价为______元,利润为______元,商场的台灯平均每月的销售量为______台
 如果商场要想销售利润平均每月达到10000,商场经理甲说:“在原售价每台50元的基础上再上涨25元,可以完成任务”,商场经理乙说:“不用涨那么多,在原售价每台50元的基础上再上涨15元就可以了”,为减少库存,应该采取谁的意见?
如果商场要想销售利润平均每月达到10000,商场经理甲说:“在原售价每台50元的基础上再上涨25元,可以完成任务”,商场经理乙说:“不用涨那么多,在原售价每台50元的基础上再上涨15元就可以了”,为减少库存,应该采取谁的意见? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,函数y=
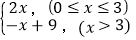 的图象与双曲线y=
的图象与双曲线y=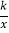 (k≠0,x>0)相交于点A(3,m)和点B.
(k≠0,x>0)相交于点A(3,m)和点B.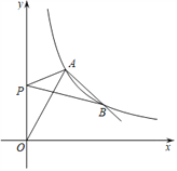
(1)求双曲线的解析式及点B的坐标;
(2)若点P在y轴上,连接PA,PB,求当PA+PB的值最小时点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,矩形ABCD中,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O.
(1)如图1,连接AF、CE,求证:四边形AFCE为菱形;
(2)如图2,若AB=4cm,AF=5cm,动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周,即点P自A→F→B→A停止,点Q自C→D→E→C停止,在运动过程中:
①已知点P的速度为每秒5cm,点Q的速度为每秒4cm,运动时间为
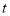 秒,当A、C、P、Q四点为顶点的四边形是平行四边形时,求
秒,当A、C、P、Q四点为顶点的四边形是平行四边形时,求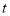 的值;
的值;②若点P、Q的运动路程分别为
 (单位:cm,
(单位:cm, ),已知A、C、P、Q四点为顶点的四边形是平行四边形,求
),已知A、C、P、Q四点为顶点的四边形是平行四边形,求 与
与 满足的数量关系式。
满足的数量关系式。
-
科目: 来源: 题型:
查看答案和解析>>【题目】下图反映的过程是小明从家去菜地浇水,又去玉米地锄草,然后回家.其中x表示时间,y表示小明离他家的距离.根据图象回答下列问题:

①菜地离小明家多远?小明走到菜地用了多少时间?
②小明给菜地浇水用了多少时间?
③玉米地离菜地、小明家多远?小明从玉米地走回家平均速度是多少?
相关试题

