【题目】已知,矩形ABCD中,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O.
(1)如图1,连接AF、CE,求证:四边形AFCE为菱形;
(2)如图2,若AB=4cm,AF=5cm,动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周,即点P自A→F→B→A停止,点Q自C→D→E→C停止,在运动过程中:
①已知点P的速度为每秒5cm,点Q的速度为每秒4cm,运动时间为![]() 秒,当A、C、P、Q四点为顶点的四边形是平行四边形时,求
秒,当A、C、P、Q四点为顶点的四边形是平行四边形时,求![]() 的值;
的值;
②若点P、Q的运动路程分别为![]() (单位:cm,
(单位:cm,![]() ),已知A、C、P、Q四点为顶点的四边形是平行四边形,求
),已知A、C、P、Q四点为顶点的四边形是平行四边形,求![]() 与
与![]() 满足的数量关系式。
满足的数量关系式。

参考答案:
【答案】(1)见解析;(2)①![]() ;②a+b=12(ab≠0).
;②a+b=12(ab≠0).
【解析】
(1)证明△AOE≌△COF,由全等推出OE=OF,得出平行四边形AFCE,再根据对角线互相垂直平分的平行四边形是菱形即可得结论;
(2)①分情况讨论可知,P点在BF上,Q点在ED上时,才能构成平行四边形,根据平行四边形的性质列出方程求解即可;
②由题意得,以A、C、P、O四点为顶点的四边形是平行四边形时,点P、Q在互相平行的对应边上,分三种情况,画出图形讨论即可得.
(1)∵四边形ABCD是矩形,
∴AE∥FC,
∴∠EAO=∠FCO,
∵EF垂直平分AC,
∴AO=CO,FE⊥AC,
在△AOE和△COF中
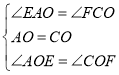 ,
,
∴△AOE≌△COF,
∴EO=FO,
∴四边形AFCE为平行四边形,
又∵FE⊥AC,
∴平行四边形AFCE为菱形;
(2)①显然当P点在AF上时,Q点在CD上,此时A、C、P、Q四点不可能构成平行四边形;
同理P点在AB上时,Q点在DE或CE上,也不能构成平行四边形,
因此只有当P点在BF上,Q点在ED上时,才能构成平行四边形,
∴以A、C、P、O四点为顶点的四边形是平行四边形时,PC=QA,
∵点P的速度为每秒5cm,点Q的速度为每秒4cm,运动时间为t秒,
∴PC=5t,QA=12-4t, ∴5t=12-4t,解得:t=![]() ,
,
∴以A、C、P、O四点为顶点的四边形是平行四边形时,t=![]() ;
;
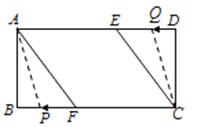
②由题意得,以A、C、P、O四点为顶点的四边形是平行四边形时,点P、Q在互相平行的对应边上,
分三种情况:
(i)如图1,当P点在AF上,Q点在CE上时,AP=CQ,即a=12-b,得a+b=12;
(ii) 如图2,当P点在BF上,Q点在DE上时,AQ=CP,即12-b=a,得a+b=12;
(iii) 如图3,当P点在AB上,Q点在CD上时,AP=CQ,即12-a=b,得a+b=12;
综上所述,a与b满足的数量关系式是a+b=12(ab≠0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场将进货价为35元台灯以50元销售价售出,平均每月能售出500个,市场调研表明:当销售价每上涨1元时,其销售量就将减少10个
 若设每个台灯的销售价上涨a元.
若设每个台灯的销售价上涨a元. 试用含a的代数式填空:涨价后,每个台灯的销售价为______元,利润为______元,商场的台灯平均每月的销售量为______台
试用含a的代数式填空:涨价后,每个台灯的销售价为______元,利润为______元,商场的台灯平均每月的销售量为______台
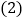 如果商场要想销售利润平均每月达到10000,商场经理甲说:“在原售价每台50元的基础上再上涨25元,可以完成任务”,商场经理乙说:“不用涨那么多,在原售价每台50元的基础上再上涨15元就可以了”,为减少库存,应该采取谁的意见?
如果商场要想销售利润平均每月达到10000,商场经理甲说:“在原售价每台50元的基础上再上涨25元,可以完成任务”,商场经理乙说:“不用涨那么多,在原售价每台50元的基础上再上涨15元就可以了”,为减少库存,应该采取谁的意见? -
科目: 来源: 题型:
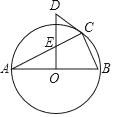
查看答案和解析>>【题目】如图,△ABC内接于⊙O,且AB为⊙O的直径OD⊥AB,与AC交于点E,与过点C的⊙O切线交于点D.
(1)若AC=6,BC=3,求OE的长.
(2)试判断∠A与∠CDE的数量关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,函数y=
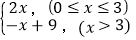 的图象与双曲线y=
的图象与双曲线y=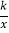 (k≠0,x>0)相交于点A(3,m)和点B.
(k≠0,x>0)相交于点A(3,m)和点B.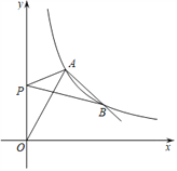
(1)求双曲线的解析式及点B的坐标;
(2)若点P在y轴上,连接PA,PB,求当PA+PB的值最小时点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下图反映的过程是小明从家去菜地浇水,又去玉米地锄草,然后回家.其中x表示时间,y表示小明离他家的距离.根据图象回答下列问题:

①菜地离小明家多远?小明走到菜地用了多少时间?
②小明给菜地浇水用了多少时间?
③玉米地离菜地、小明家多远?小明从玉米地走回家平均速度是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】为推动阳光体育活动的广泛开展,引导学生积极参加体育锻炼,学校准备购买一批运动鞋供学生借用.现从各年级随机抽取了部分学生的鞋号,绘制了如下的统计图①和图②,请根据图中提供的信息,解答下列问题:

(1)本次接受随机抽样调查的学生人数为 人,图①中的m的值为 ,图①中“38号”所在的扇形的圆心角度数为 ;
(2)本次调查获取的样本数据的众数是 ,中位数是 ;
(3)根据样本数据,若学校计划购买200双运动鞋,建议购买36号运动鞋多少双?
-
科目: 来源: 题型:
查看答案和解析>>【题目】求知中学有一块四边形的空地ABCD,如下图所示,学校计划在空地上种植草皮,经测量∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m,若每平方米草皮需要250元,问学校需要投入多少资金买草皮?

相关试题

