【题目】在△ABC中,点D、E分别在边AC、BC上(不与点A、B、C重合),点P是直线AB上的任意一点(不与点A、B重合).设∠PDA=x,∠PEB=y,∠DPE=m,∠C=n.
(1)如图,当点P在线段AB上运动,且n=90°时
①若PD∥BC,PE∥AC,则m=_____;
②若m=50°,求x+y的值.
(2)当点P在直线AB上运动时,直接写出x、y、m、n之间的数量关系.


参考答案:
【答案】(1)①90°,②140°;(2)详见解析.
【解析】分析:(1)①证明四边形DPEC为平行四边形可得结论;
②根据四边形内角和为360°,列等式求出x+y的值;
(2)根据P、D、E位置的不同,分五种情况:①y-x=m+n,如图2,点P在BA的延长线上时,根据三角形的内角和与外角定理列等式,化简后得出结论;
②x-y=m-n,如图3,点P在BA的延长线上时,根据三角形的内角和与外角定理列等式,化简后得出结论;
③x+y=m+n,如图4,点P在线段BA上时,根据四边形的内角和为360°列等式,化简后得出结论;
④x-y=m+n,如图5,同理得出结论;
⑤y-x=m-n,如图6,同理得出结论.
详解:(1)①如图1,
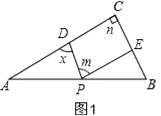
∵PD∥BC,PE∥AC,
∴四边形DPEC为平行四边形,
∴∠DPE=∠C,
∵∠DPE=m,∠C=n=90°,
∴m=90°;
②∵∠ADP=x,∠PEB=y,
∴∠CDP=180°-x,∠CEP=180°-y,
∵∠C+∠CDP+∠DPE+∠CEP=360°,
∠C=90°,∠DPE=50°,
∴90°+180°-x+50°+180°-y=360°,
∴x+y=140°;
(2)分五种情况:
①y﹣x=m+n,如图2,
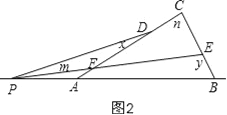
理由是:
∵∠DFP=n+∠FEC,∠FEC=180°﹣y,
∴∠DFP=n+180°﹣y,
∵x+m+∠DFP=180°,
∴x+m+n+180°﹣y=180°,
∴y﹣x=m+n;
②x﹣y=m﹣n,如图3,
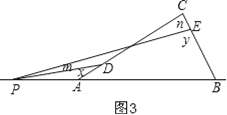
理由是:
同理得:m+180°﹣x=n+180°﹣y,
∴x﹣y=m﹣n;
③x+y=m+n,如图4,

理由是:
由四边形内角和为360°得:180°﹣x+m+180°﹣y+n=360°,
∴x+y=m+n;
④x﹣y=m+n,如图5,
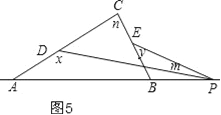
理由是:
同理得:180°=m+n+y+180°﹣x,
∴x﹣y=m+n;
⑤y﹣x=m﹣n,如图6,
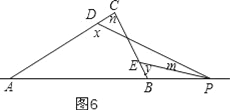
理由是:
同理得:n+180°﹣x=m+180°﹣y,
∴y﹣x=m﹣n.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知代数式A=x2+3xy+x-
 ,B=2x2-xy+4y-1
,B=2x2-xy+4y-1(1)当x=y=-2时,求2A-B的值;
(2)若2A-B的值与y的取值无关,求x的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市雾霾天气趋于严重,甲商场根据民众健康需要,代理销售每台进价分别为600元、560
元的 A、B 两种型号的空气净化器,如表是近两周的销售情况:(进价、售价均保持不变,利润=销
售收入进货成本)
销售时段
销售数量
销售收入
(元)
A种型号
(台)
B种型号
(台)
第一周
3
2
3960
第二周
5
4
7120
(1)求 A,B 两种型号的空气净化器的销售单价;
(2)该商店计划一次购进两种型号的空气净化器共30台,其中B型净化器的进货量不超过A型的2倍.设购进A型空气净化器为x台,这30台空气净化器的销售总利润为y元.
①请写出y关于x的函数关系式;
②该商店购进A型、B型净化器各多少台,才能使销售总利润最大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公园准备修建一块长方形草坪,长为30米,宽为20米.并在草坪上修建如图所示的十字路,已知十字路宽
 米,回答下列问题:
米,回答下列问题:(1)修建十字路的面积是多少平方米?
(2)草坪(阴影部分)的面积是多少?
(3)如果十字路宽2米,那么草坪(阴影部分)的面积是多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB为⊙O的直径,C为⊙O上一点,弦AD平分∠BAC,交BC于点E,AB=6,AD=5,则AE的长为( )
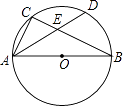
A.2.5
B.2.8
C.3
D.3.2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A、B和线段MN都在数轴上,点A、M、N、B对应的数字分别为﹣1、0、2、11.线段MN沿数轴的正方向以每秒1个单位的速度移动,移动时间为t秒.
(1)用含有t的代数式表示AM的长为
(2)当t= 秒时,AM+BN=11.
(3)若点A、B与线段MN同时移动,点A以每秒2个单位速度向数轴的正方向移动,点B以每秒1个单位的速度向数轴的负方向移动,在移动过程,AM和BN可能相等吗?若相等,请求出t的值,若不相等,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,己知△ABC中,AB=3,AC=4,BC=5,作∠ABC的角平分线交AC于D,以D为圆心,DA为半径作圆,与射线交于点E、F.有下列结论: ①△ABC是直角三角形;②⊙D与直线BC相切;③点E是线段BF的黄金分割点;④tan∠CDF=2.
其中正确的结论有( )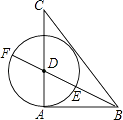
A.4个
B.3个
C.2个
D.1个
相关试题

