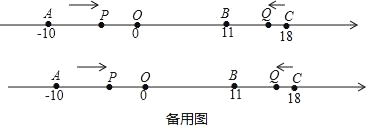
【题目】如图,在数轴上,点A表示﹣10,点B表示11,点C表示18.动点P从点A出发,沿数轴正方向以每秒2个单位的速度匀速运动;同时,动点Q从点C出发,沿数轴负方向以每秒1个单位的速度匀速运动.设运动时间为t秒.
(1)当t为何值时,P、Q两点相遇?相遇点M所对应的数是多少?
(2)在点Q出发后到达点B之前,求t为何值时,点P到点O的距离与点Q到点B的距离相等;
(3)在点P向右运动的过程中,N是AP的中点,在点P到达点C之前,求2CN﹣PC的值.
参考答案:
【答案】(1)t=![]() , M所对应的数是
, M所对应的数是![]() ;(2)t的值为3或
;(2)t的值为3或![]() ;(3)28.
;(3)28.
【解析】
(1) 根据题意, 由P、 Q两点的路程和为28路程方程求解即可;
(2) 由题意得,t的值大于0且小于7. 分点P在点O的左边, 点P在点O的右边两种情况讨论即可求解;
(3) 根据中点的定义得到AN=PN=![]() AP=t,可得CN=AC-AN=28-t, PC=28-AP=28-2t, 再代入计算即可求解.
AP=t,可得CN=AC-AN=28-t, PC=28-AP=28-2t, 再代入计算即可求解.
解:(1)根据题意得2t+t=28,
解得t=![]() ,
,
∴AM=![]() >10,
>10,
∴M在O的右侧,且OM=![]() ﹣10=
﹣10=![]() ,
,
∴当t=![]() 时,P、Q两点相遇,相遇点M所对应的数是
时,P、Q两点相遇,相遇点M所对应的数是![]() ;
;
(2)由题意得,t的值大于0且小于7.
若点P在点O的左边,则10﹣2t=7﹣t,解得t=3.
若点P在点O的右边,则2t﹣10=7﹣t,解得t=![]() .
.
综上所述,t的值为3或![]() 时,点P到点O的距离与点Q到点B的距离相等;
时,点P到点O的距离与点Q到点B的距离相等;
(3)∵N是AP的中点,
∴AN=PN=![]() AP=t,
AP=t,
∴CN=AC﹣AN=28﹣t,PC=28﹣AP=28﹣2t,
2CN﹣PC=2(28﹣t)﹣(28﹣2t)=28.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A、B都在数轴上,O为原点.
(1)点B表示的数是_________________;
(2)若点B以每秒2个单位长度的速度沿数轴向右运动,则2秒后点B表示的数是________;
(3)若点A、B分别以每秒1个单位长度、3个单位长度的速度沿数轴向右运动,而点O不动,t秒后,A、B、O三个点中有一个点是另外两个点为端点的线段的中点,求t的值.
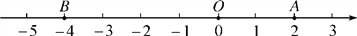
-
科目: 来源: 题型:
查看答案和解析>>【题目】“低碳环保,你我同行”.仪征市区的公共自行车给市民出行带来不少方便.我校数学社团小学员走进小区随机选取了市民进行调查,调查的问题是“您大概多久使用一次公共自行车?”,将本次调查结果归为四种情况: A.每天都用;B.经常使用;C.偶尔使用;D.从未使用.
将这次调查情况整理并绘制如下两幅统计图: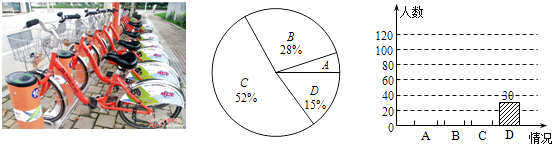
根据图中的信息,解答下列问题:
(1)本次活动共有位市民参与调查;
(2)补全条形统计图;
(3)根据统计结果,若市区有26万市民,请估算每天都用公共自行车的市民约有多少人? -
科目: 来源: 题型:
查看答案和解析>>【题目】我校“文化氧吧”有A、B、C、D四本书是小明想拜读的,但他现阶段只打算选读两本.
(1)若小明已选A书,再从其余三本书中随机选一款,恰好选中C的概率是;
(2)小明随机选取两本书,请用树状图或列表法求出他恰好选中A、C两本的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】某星期天下午,小强和小明相约在某公共汽车站一起乘车回学校,小强从家出发先步行到车站,等小明到了后两人一起乘公共汽车回到学校.图中折线表示小强离开家的路程
 (公里)和所用时间
(公里)和所用时间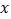 (分钟)之间的函数关系.下列说法中错误的是( )
(分钟)之间的函数关系.下列说法中错误的是( )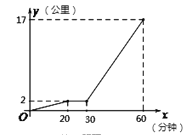
A. 小强从家到公共汽车站步行了2公里 B. 小强在公共汽车站等小明用了10分钟
C. 小强乘公共汽车用了20分钟 D. 公共汽车的平均速度是30公里/小时
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,四边形ABCD和四边形AECF都是矩形,AE与BC交于点M,CF与AD交于点N.
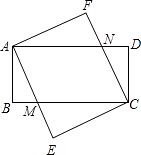
(1)求证:△ABM≌△CDN;
(2)矩形ABCD和矩形AECF满足何种关系时,四边形AMCN是菱形,证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两个公司为某敬老院各捐款300000元.已知甲公司的人数比乙公司的人数多20%,乙公司比甲公司人均多捐款20元.则甲、乙两公司各有多少元?
相关试题

