【题目】解下列方程:
(1)(2x-1)2=4
(2)![]() (用配方法)
(用配方法)
(3)x2+2x=4.
(4)![]()
参考答案:
【答案】
(1)解:∵(2x-1)2=4,
∴2x-1=2或2x-1=-2,
∴x1= ![]() ,x2=-
,x2=- ![]() ,
,
(2)解:∵x2-4x+1=0,
∴x2-4x+4=-1+4,
∴(x-2)2=3,
∴x1= ![]() , x2=
, x2= ![]() ,
,
(3)解:∵x2+2x=4,
∴x2+2x+1=4+1,
∴(x+1)2=5,
∴x1=-1+ ![]() ,x2=-1-
,x2=-1- ![]() ,
,
(4)解:∵2 ( x 3 ) 2 = x ( x 3 ),
∴(x-3)【2(x-3)-x】=0,
∴(x-3)(x-6)=0,
∴x1=3,x2=6,
【解析】(1)根据一元二次方程的解法——直接开平方法解方程即可.
(2)根据一元二次方程的解法——配方法和直接开平方法解方程即可.
(3)根据一元二次方程的解法——配方法和直接开平方法解方程即可.
(4)根据一元二次方程的解法——因式分解法解方程即可.
【考点精析】关于本题考查的直接开平方法和配方法,需要了解方程没有一次项,直接开方最理想.如果缺少常数项,因式分解没商量.b、c相等都为零,等根是零不要忘.b、c同时不为零,因式分解或配方,也可直接套公式,因题而异择良方;左未右已先分离,二系化“1”是其次.一系折半再平方,两边同加没问题.左边分解右合并,直接开方去解题才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】A市准备争创全国卫生城市.某小区积极响应,决定在小区内安装垃圾分类的提示牌和垃圾箱,若购买2个提示牌和3个垃圾箱共需550元,且垃圾箱的单价是提示牌单价的3倍.
(1)求提示牌和垃圾箱的单价各是多少元?
(2)该小区至少需要安放48个垃圾箱,如果购买提示牌和垃圾箱共100个,且费用不超过10000元,请你列举出所有购买方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,MN是⊙O的直径,MN=2,点A在⊙O上,∠AMN=30°,B为弧AN的中点,P是直径MN上一动点,则PA+PB的最小值为 .
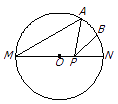
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,甲长方形的两边长分别为
 ,
, ;乙长方形的两边长分别为
;乙长方形的两边长分别为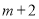 ,
, .(其中
.(其中 为正整数)
为正整数)
(1)图中的甲长方形的面积
 ,乙长方形的面积
,乙长方形的面积 ,比较:
,比较: 
 (填“<”、“=”或“>”);
(填“<”、“=”或“>”);(2)现有一正方形,其周长与图中的甲长方形周长相等,试探究:该正方形面积
 与图中的甲长方形面积
与图中的甲长方形面积 的差(即
的差(即 )是一个常数,求出这个常数;
)是一个常数,求出这个常数;(3)在(1)的条件下,若某个图形的面积介于
 、
、 之间(不包括
之间(不包括 、
、 )并且面积为整数,这样的整数值有且只有16个,求
)并且面积为整数,这样的整数值有且只有16个,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:关于x的方程x2+2mx+m2﹣1=0
(1)不解方程,判别方程根的情况;
(2)若方程有一个根为3,求m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】好学的小红在学完三角形的角平分线后,遇到下列4个问题,请你帮她解决.如图,在
 中,点
中,点 是
是 、
、 的平分线的交点,点
的平分线的交点,点 是
是 、
、 平分线的交点,
平分线的交点, 的延长线交于点
的延长线交于点 .
.
(1)若
 ,则
,则 °;
°;(2)若
 (
( ),则当
),则当 等于多少度(用含
等于多少度(用含 的代数式表示)时,
的代数式表示)时, ,并说明理由;
,并说明理由;(3)若
 ,求
,求 的度数.
的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】在等腰△ABC中,三边分别为a、b、c,其中
 ,若关于x的方程
,若关于x的方程 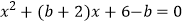 有两个相等的实数根,求△ABC的周长.
有两个相等的实数根,求△ABC的周长.
相关试题

