【题目】如图,甲长方形的两边长分别为![]() ,
,![]() ;乙长方形的两边长分别为
;乙长方形的两边长分别为![]() ,
,![]() .(其中
.(其中![]() 为正整数)
为正整数)

(1)图中的甲长方形的面积![]() ,乙长方形的面积
,乙长方形的面积![]() ,比较:
,比较: ![]()
![]() (填“<”、“=”或“>”);
(填“<”、“=”或“>”);
(2)现有一正方形,其周长与图中的甲长方形周长相等,试探究:该正方形面积![]() 与图中的甲长方形面积
与图中的甲长方形面积![]() 的差(即
的差(即![]() )是一个常数,求出这个常数;
)是一个常数,求出这个常数;
(3)在(1)的条件下,若某个图形的面积介于![]() 、
、![]() 之间(不包括
之间(不包括![]() 、
、![]() )并且面积为整数,这样的整数值有且只有16个,求
)并且面积为整数,这样的整数值有且只有16个,求![]() 的值.
的值.
参考答案:
【答案】(1)>;(2)9;(3)9.
【解析】
(1)根据矩形的面积公式计算即可;
(2)根据矩形和正方形的周长和面积公式即可得到结论;
(3)根据题意列出不等式,然后求解即可得到结论.
解:(1)图①中长方形的面积![]() ,
,
图②中长方形的面积![]() ,
,
![]() ,
,![]() 为正整数,
为正整数,![]() 最小为1,
最小为1,
![]() ,
,
![]() ;
;
(2)依题意得,正方形的边长为:![]() ;
;
则:![]() ,是一个定值;
,是一个定值;
(3)由(1)得,![]() ,
,
根据某个图形的面积介于![]() 、
、![]() 之间(不包括
之间(不包括![]() 、
、![]() )并且面积为整数,这样的整数值有且只有16个,
)并且面积为整数,这样的整数值有且只有16个,
![]() 当
当![]() 时,
时,
![]()
![]() ,
,
![]() 为正整数,
为正整数,
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】晓琳和爸爸到太子河公园运动,两人同时从家出发,沿相同路线前行,途中爸爸有事返回,晓琳继续前行5分钟后也原路返回,两人恰好同时到家.晓琳和爸爸在整个运动过程中离家的路程y1(米),y2(米)与运动时间x(分)之间的函数关系如图所示,下列结论:①两人同行过程中的速度为200米/分;②m的值是15,n的值是3000;③晓琳开始返回时与爸爸相距1800米;④运动18分钟或30分钟时,两人相距900米.其中正确结论的个数是( )
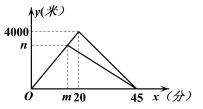
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】A市准备争创全国卫生城市.某小区积极响应,决定在小区内安装垃圾分类的提示牌和垃圾箱,若购买2个提示牌和3个垃圾箱共需550元,且垃圾箱的单价是提示牌单价的3倍.
(1)求提示牌和垃圾箱的单价各是多少元?
(2)该小区至少需要安放48个垃圾箱,如果购买提示牌和垃圾箱共100个,且费用不超过10000元,请你列举出所有购买方案.
-
科目: 来源: 题型:
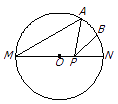
查看答案和解析>>【题目】如图,MN是⊙O的直径,MN=2,点A在⊙O上,∠AMN=30°,B为弧AN的中点,P是直径MN上一动点,则PA+PB的最小值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列方程:
(1)(2x-1)2=4
(2)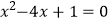 (用配方法)
(用配方法)
(3)x2+2x=4.
(4)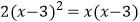
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:关于x的方程x2+2mx+m2﹣1=0
(1)不解方程,判别方程根的情况;
(2)若方程有一个根为3,求m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】好学的小红在学完三角形的角平分线后,遇到下列4个问题,请你帮她解决.如图,在
 中,点
中,点 是
是 、
、 的平分线的交点,点
的平分线的交点,点 是
是 、
、 平分线的交点,
平分线的交点, 的延长线交于点
的延长线交于点 .
.
(1)若
 ,则
,则 °;
°;(2)若
 (
( ),则当
),则当 等于多少度(用含
等于多少度(用含 的代数式表示)时,
的代数式表示)时, ,并说明理由;
,并说明理由;(3)若
 ,求
,求 的度数.
的度数.
相关试题

