【题目】好学的小红在学完三角形的角平分线后,遇到下列4个问题,请你帮她解决.如图,在![]() 中,点
中,点![]() 是
是![]() 、
、![]() 的平分线的交点,点
的平分线的交点,点![]() 是
是![]() 、
、![]() 平分线的交点,
平分线的交点,![]() 的延长线交于点
的延长线交于点![]() .
.

(1)若![]() ,则
,则![]() °;
°;
(2)若![]() (
(![]() ),则当
),则当![]() 等于多少度(用含
等于多少度(用含![]() 的代数式表示)时,
的代数式表示)时,![]() ,并说明理由;
,并说明理由;
(3)若![]() ,求
,求![]() 的度数.
的度数.
参考答案:
【答案】(1)115;(2)180-2x,理由见解析;(3)45°.
【解析】
(1)已知点I是两角∠ABC 、∠ACB平分线的交点,故![]()
,由此可求∠BIC;
(2)当CE∥AB时, ∠ACE=∠A=x°,根据∠ACE=∠A=x°,根据CE是∠ACG的角平分线,推出∠ACG=2x°,∠ABC=∠BAC=x°,即可求出![]() 的度数.
的度数.
(3)由题意知:△BDE是直角三角形∠D+∠E=90°,可求出若∠D=3∠E时,∠BEC=22.5°,再推理出![]() ,即可求出
,即可求出![]() 的度数.
的度数.
(1)∵点I是两角∠ABC 、∠ACB平分线的交点,
∴![]()
![]()
![]()
![]() ;
;
故答案为:115.
(2)当∠ACB等于(180-2x)°时,CE∥AB.理由如下:
∵CE∥AB,
∴∠ACE=∠A=x°,
∵∠ACE=∠A=x°,CE是∠ACG的角平分线,
∴∠ACG=2∠ACE=2x°,
∴∠ABC=∠ACG-∠BAC=2x°-x°=x°,
∴∠ACB=180°-∠BAC-∠ABC=(180-2x)°;
(3)由题意知:△BDE是直角三角形∠D+∠E=90°
若∠D=3∠E时∠BEC=22.5°,
∵![]()
![]()
![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,甲长方形的两边长分别为
 ,
, ;乙长方形的两边长分别为
;乙长方形的两边长分别为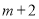 ,
, .(其中
.(其中 为正整数)
为正整数)
(1)图中的甲长方形的面积
 ,乙长方形的面积
,乙长方形的面积 ,比较:
,比较: 
 (填“<”、“=”或“>”);
(填“<”、“=”或“>”);(2)现有一正方形,其周长与图中的甲长方形周长相等,试探究:该正方形面积
 与图中的甲长方形面积
与图中的甲长方形面积 的差(即
的差(即 )是一个常数,求出这个常数;
)是一个常数,求出这个常数;(3)在(1)的条件下,若某个图形的面积介于
 、
、 之间(不包括
之间(不包括 、
、 )并且面积为整数,这样的整数值有且只有16个,求
)并且面积为整数,这样的整数值有且只有16个,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】解下列方程:
(1)(2x-1)2=4
(2)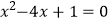 (用配方法)
(用配方法)
(3)x2+2x=4.
(4)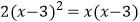
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:关于x的方程x2+2mx+m2﹣1=0
(1)不解方程,判别方程根的情况;
(2)若方程有一个根为3,求m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在等腰△ABC中,三边分别为a、b、c,其中
 ,若关于x的方程
,若关于x的方程 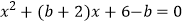 有两个相等的实数根,求△ABC的周长.
有两个相等的实数根,求△ABC的周长. -
科目: 来源: 题型:
查看答案和解析>>【题目】下图是某班学生外出乘车、步行、骑车的人数条形统计图和扇形分布图。


(1)求该班有多少名学生?
(2)补上步行分布直方图的空缺部分;
(3)在扇形统计图中,求骑车人数所占的圆心角度数。
(4)若全年级有 800 人,估计该年级步行人数。
-
科目: 来源: 题型:
查看答案和解析>>【题目】某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面的半径,下图是水平放置的破裂管道有水部分的截面.

(1)请你补全这个输水管道的圆形截面;
(2)若这个输水管道有水部分的水面宽AB=16cm,水面最深地方的高度为4cm,求这个圆形截面的半径.
相关试题

