【题目】在等腰△ABC中,三边分别为a、b、c,其中 ![]() ,若关于x的方程
,若关于x的方程 ![]() 有两个相等的实数根,求△ABC的周长.
有两个相等的实数根,求△ABC的周长.
参考答案:
【答案】解:∵方程有两个相等的实数根,
∴△=b2-4ac=(b+2)2-4×1×(6-b)=0,
∴b2+8b-20=0,
∴(b+10)(b-2)=0
∴b1=-10,b2=2,
又∵b为等腰△ABC的边,
∴b=2,
又∵a=5,
∴a=c=5,
∴C△ABC=2+5+5=12.
故答案为:12.
【解析】根据一元二次方程根的判别式结合题意求出b的值,再根据等腰三角形的性质以及三角形三边的关系求出△ABC的周长.
【考点精析】本题主要考查了求根公式和三角形三边关系的相关知识点,需要掌握根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根;三角形两边之和大于第三边;三角形两边之差小于第三边;不符合定理的三条线段,不能组成三角形的三边才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解下列方程:
(1)(2x-1)2=4
(2)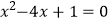 (用配方法)
(用配方法)
(3)x2+2x=4.
(4)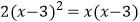
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:关于x的方程x2+2mx+m2﹣1=0
(1)不解方程,判别方程根的情况;
(2)若方程有一个根为3,求m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】好学的小红在学完三角形的角平分线后,遇到下列4个问题,请你帮她解决.如图,在
 中,点
中,点 是
是 、
、 的平分线的交点,点
的平分线的交点,点 是
是 、
、 平分线的交点,
平分线的交点, 的延长线交于点
的延长线交于点 .
.
(1)若
 ,则
,则 °;
°;(2)若
 (
( ),则当
),则当 等于多少度(用含
等于多少度(用含 的代数式表示)时,
的代数式表示)时, ,并说明理由;
,并说明理由;(3)若
 ,求
,求 的度数.
的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】下图是某班学生外出乘车、步行、骑车的人数条形统计图和扇形分布图。


(1)求该班有多少名学生?
(2)补上步行分布直方图的空缺部分;
(3)在扇形统计图中,求骑车人数所占的圆心角度数。
(4)若全年级有 800 人,估计该年级步行人数。
-
科目: 来源: 题型:
查看答案和解析>>【题目】某居民小区一处圆柱形的输水管道破裂,维修人员为更换管道,需确定管道圆形截面的半径,下图是水平放置的破裂管道有水部分的截面.

(1)请你补全这个输水管道的圆形截面;
(2)若这个输水管道有水部分的水面宽AB=16cm,水面最深地方的高度为4cm,求这个圆形截面的半径. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BD相交于点N,连接BM,DN.

(1)求证:四边形BMDN是菱形;
(2)若AB=4,AD=8,求MD的长
相关试题

