【题目】如图,MN是⊙O的直径,MN=2,点A在⊙O上,∠AMN=30°,B为弧AN的中点,P是直径MN上一动点,则PA+PB的最小值为 . 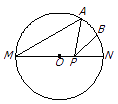
参考答案:
【答案】![]()
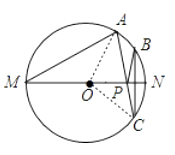
【解析】作点B关于MN的对称点C,连接AC交NM于点P,则P点就是所作的点;
∴PB=PC,
∴PA+PB=PA+PC=AC,
即此时PA+PB最小,
连接OA,OC,
∵∠AMN=30°,
∴∠AON=60°,
∴弧AN的度数为60°,
又∵B为弧AN的中点,
∴弧BN的度数为30°,
又∵点B关于MN的对称点为C,
∴弧CN的度数为30°,
∴∠AOC=90°,
又∵MN是⊙O的直径,MN=2,
∴OA=OC=1,
∴AC=![]() =
=![]() .
.
所以答案是:![]() .
.
【考点精析】利用勾股定理的概念和圆心角、弧、弦的关系对题目进行判断即可得到答案,需要熟知直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等;在同圆或等圆中,同弧等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在方格纸内将
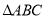 水平向右平移4个单位得到
水平向右平移4个单位得到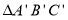 .
.(1)补全
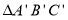 ,利用网格点和直尺画图;
,利用网格点和直尺画图;(2)图中
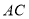 与
与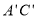 的位置关系是: ;
的位置关系是: ;(3)画出
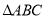 中
中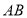 边上的中线
边上的中线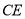 ;
;(4)平移过程中,线段
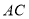 扫过的面积是: .
扫过的面积是: .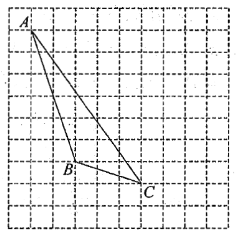
-
科目: 来源: 题型:
查看答案和解析>>【题目】晓琳和爸爸到太子河公园运动,两人同时从家出发,沿相同路线前行,途中爸爸有事返回,晓琳继续前行5分钟后也原路返回,两人恰好同时到家.晓琳和爸爸在整个运动过程中离家的路程y1(米),y2(米)与运动时间x(分)之间的函数关系如图所示,下列结论:①两人同行过程中的速度为200米/分;②m的值是15,n的值是3000;③晓琳开始返回时与爸爸相距1800米;④运动18分钟或30分钟时,两人相距900米.其中正确结论的个数是( )
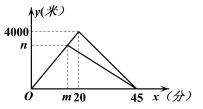
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】A市准备争创全国卫生城市.某小区积极响应,决定在小区内安装垃圾分类的提示牌和垃圾箱,若购买2个提示牌和3个垃圾箱共需550元,且垃圾箱的单价是提示牌单价的3倍.
(1)求提示牌和垃圾箱的单价各是多少元?
(2)该小区至少需要安放48个垃圾箱,如果购买提示牌和垃圾箱共100个,且费用不超过10000元,请你列举出所有购买方案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,甲长方形的两边长分别为
 ,
, ;乙长方形的两边长分别为
;乙长方形的两边长分别为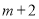 ,
, .(其中
.(其中 为正整数)
为正整数)
(1)图中的甲长方形的面积
 ,乙长方形的面积
,乙长方形的面积 ,比较:
,比较: 
 (填“<”、“=”或“>”);
(填“<”、“=”或“>”);(2)现有一正方形,其周长与图中的甲长方形周长相等,试探究:该正方形面积
 与图中的甲长方形面积
与图中的甲长方形面积 的差(即
的差(即 )是一个常数,求出这个常数;
)是一个常数,求出这个常数;(3)在(1)的条件下,若某个图形的面积介于
 、
、 之间(不包括
之间(不包括 、
、 )并且面积为整数,这样的整数值有且只有16个,求
)并且面积为整数,这样的整数值有且只有16个,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】解下列方程:
(1)(2x-1)2=4
(2)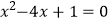 (用配方法)
(用配方法)
(3)x2+2x=4.
(4)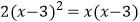
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:关于x的方程x2+2mx+m2﹣1=0
(1)不解方程,判别方程根的情况;
(2)若方程有一个根为3,求m的值.
相关试题

