【题目】如图,正方形![]() 中,
中,![]() ,
,![]() ,
,![]() 交于点
交于点![]() .若
.若![]() ,
,![]() 分别是边
分别是边![]() ,
,![]() 上的动点,且
上的动点,且![]() ,则
,则![]() 周长的最小值是__________.
周长的最小值是__________.

参考答案:
【答案】![]()
【解析】
根据正方形的对角线互相平分且相等可得AO=BO,∠AOB=90°,对角线平分一组对角可得∠OAE=∠OBF,再根据AE=BF,然后利用“SAS”证明△AOE和△BOF全等,根据全等三角形对应角相等可得∠AOE=∠BOF,可得∠EOF=90°,然后利用勾股定理列式计算即可得解.
解:在正方形ABCD中,AO=BO,∠AOB=90°,∠OAE=∠OBF=45°,
∵点E、F的速度相等,
∴AE=BF,
在△AOE和△BOF中,
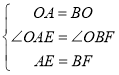 ,
,
∴△AOE≌△BOF(SAS),
∴∠AOE=∠BOF,
∴∠AOE+∠BOE=90°,
∴∠BOF+∠BOE=90°,
∴∠EOF=90°,
在Rt△BEF中,设AE=x,则BF=x,BE=2-x,
EF=![]() .
.
∴当x=1时,EF有最小值为![]() .
.
∴OE=OF=1.
∴△OEF周长的最小值=![]() .
.
故答案为:![]() .
.
-
科目: 来源: 题型:
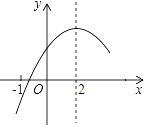
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图③所示,图象过点(﹣1,0),对称轴为直线x=2,则下 列结论中正确的个数有( )
①4a+b=0;
②9a+3b+c<0;
③若点A(﹣3,y1),点B(﹣
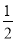 ,y2),点C(5,y3)在该函数图象上,则y1<y3<y2;
,y2),点C(5,y3)在该函数图象上,则y1<y3<y2;④若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2 , 且x1<x2 , 则x1<﹣1<5<x2 .
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在正方形
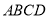 中,点
中,点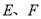 分别在
分别在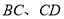 上,△
上,△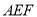 是等边三角形,连接
是等边三角形,连接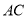 交
交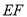 于
于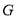 ,给出下列结论:
,给出下列结论: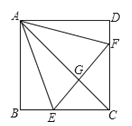
①
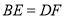 ; ②
; ② 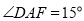 ;
;③
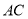 垂直平分
垂直平分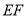 ; ④
; ④ .
.其中结论正确的共有( ).
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】使得函数值为0的自变量的值称为函数的零点.例如,对于函数y=x﹣1,令y=0可得x=1,我们说1是函数y=x﹣1的零点.已知函数y=x2﹣2mx﹣2(m+3)(m为常数)
(1)当m=0时,求该函数的零点.
(2)证明:无论m取何值,该函数总有两个零点.
-
科目: 来源: 题型:
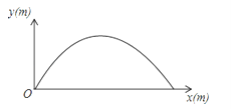
查看答案和解析>>【题目】如图,王强在一次高尔夫球的练习中,在某处击球,其飞行路线满足抛物线y=﹣
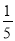 x2+
x2+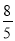 x,其中y(m)是球飞行的高度,x(m)是球飞行的水平距离.
x,其中y(m)是球飞行的高度,x(m)是球飞行的水平距离.(1)飞行的水平距离是多少时,球最高?
(2)球从飞出到落地的水平距离是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】为落实立德树人根本任务,培养德智体美劳全面发展的社会主义接班人,育才学校在设立学生奖学金时规定:每学期对学生的德智体美劳五个方面进行三次综合素质评价,分别是:假期综合素质评价、期中综合素质评价、期末综合素质评价,八年级(1)班的小明和八年级(2)班的小亮两位同学同时进入一等奖学金测评,他们的三次综合素质评价成绩如下表.
假期综合素质评价成绩
期中综合素质评价成绩
期末综合素质评价成绩
小明
96
91
92
小亮
95
93
91
(1)如果从三次综合素质评价成绩稳定性的角度来看,谁可以得一等奖学金?请你通过计算回答;
(2)如果假期综合素质评价成绩、期中综合素质评价成绩、期末综合素质评价成绩按
 的比例计入最终成绩,谁可以得一等奖学金?请你通过计算回答.
的比例计入最终成绩,谁可以得一等奖学金?请你通过计算回答. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,O为坐标原点,直线y=﹣x﹣3与x轴交于点A,与y轴交于点C,抛物线y=x2+bx+c经过A、C两点,与x轴交于另一点B
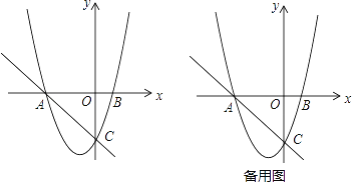
(1)求抛物线的解析式;
(2)点D是第二象限抛物线上的一个动点,连接AD、BD、CD,当S△ACD=
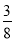 S四边形ACBD时,求D点坐标;
S四边形ACBD时,求D点坐标; (3)在(2)的条件下,连接BC,过点D作DE⊥BC,交CB的延长线于点E,点P是第三象限抛物线上的一个动点,点P关于点B的对称点为点Q,连接QE,延长QE与抛物线在A、D之间的部分交于一点F,当∠DEF+∠BPC=∠DBE时,求EF的长.
相关试题

