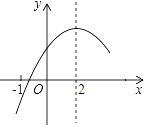
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图③所示,图象过点(﹣1,0),对称轴为直线x=2,则下 列结论中正确的个数有( )
①4a+b=0;
②9a+3b+c<0;
③若点A(﹣3,y1),点B(﹣![]() ,y2),点C(5,y3)在该函数图象上,则y1<y3<y2;
,y2),点C(5,y3)在该函数图象上,则y1<y3<y2;
④若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2 , 且x1<x2 , 则x1<﹣1<5<x2 .
A. 1个 B. 2个 C. 3个 D. 4个
参考答案:
【答案】C
【解析】试题分析:对称轴为直线x=2,则![]() ,则4a+b=0,则①正确;当x=3时函数值为正数,即
,则4a+b=0,则①正确;当x=3时函数值为正数,即![]() ,则②错误;对于开口向下的函数,离对称轴越远,则函数值越小,则
,则②错误;对于开口向下的函数,离对称轴越远,则函数值越小,则![]() ,则③正确;根据函数图像可知:当y=-3时,
,则③正确;根据函数图像可知:当y=-3时, ![]() ,则④正确;故本题选C.
,则④正确;故本题选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.

(1)求证:AF=DC;
(2)若AB⊥AC,试判断四边形ADCF的形状,并证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用适当的方法解下列方程:
(1)(6x-1)2=25;
(2)x2-2x=2x-1;
(3)x2-
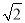 x=2;
x=2;(4)x(x-7)=8(7-x).
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着科技的发展,某快递公司为了提高分拣包裹的速度,使用机器人代替人工进行包裹分拣,若甲机器人工作
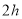 ,乙机器人工作
,乙机器人工作 ,一共可以分拣700件包裹;若甲机器人工作
,一共可以分拣700件包裹;若甲机器人工作 ,乙机器人工作
,乙机器人工作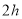 ,一共可以分拣650件包裹.
,一共可以分拣650件包裹.(1)求甲、乙两机器人每小时各分拣多少件包裹;
(2)去年“双十一”期间,快递公司的业务量猛增,为了让甲、乙两机器人每天分拣包裹的总数量不低于2250件,则它们每天至少要一起工作多少小时?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在正方形
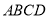 中,点
中,点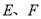 分别在
分别在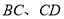 上,△
上,△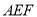 是等边三角形,连接
是等边三角形,连接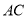 交
交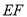 于
于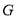 ,给出下列结论:
,给出下列结论: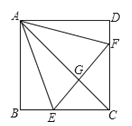
①
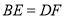 ; ②
; ② 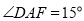 ;
;③
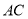 垂直平分
垂直平分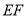 ; ④
; ④ .
.其中结论正确的共有( ).
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】使得函数值为0的自变量的值称为函数的零点.例如,对于函数y=x﹣1,令y=0可得x=1,我们说1是函数y=x﹣1的零点.已知函数y=x2﹣2mx﹣2(m+3)(m为常数)
(1)当m=0时,求该函数的零点.
(2)证明:无论m取何值,该函数总有两个零点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形
 中,
中,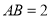 ,
,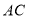 ,
,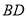 交于点
交于点 .若
.若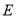 ,
,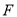 分别是边
分别是边 ,
,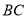 上的动点,且
上的动点,且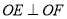 ,则
,则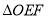 周长的最小值是__________.
周长的最小值是__________.
相关试题

