【题目】使得函数值为0的自变量的值称为函数的零点.例如,对于函数y=x﹣1,令y=0可得x=1,我们说1是函数y=x﹣1的零点.已知函数y=x2﹣2mx﹣2(m+3)(m为常数)
(1)当m=0时,求该函数的零点.
(2)证明:无论m取何值,该函数总有两个零点.
参考答案:
【答案】(1)m=0时,该函数的零点为±![]() (2)证明见解析
(2)证明见解析
【解析】试题分析:(1)、求出当y=0时的方程的解,从而得出函数的零点;(2)、利用根的判别式得出判别式为非负数,即当y=0时方程有两个不相等的实数根,即函数总有两个零点.
试题解析:(1)、解:当m=0时,令y=0,则x2﹣6=0, 解得x=±![]() ,
,
所以,m=0时,该函数的零点为±![]() ;
;
(2)、证明:令y=0,则x2﹣2mx﹣2(m+3)=0,
△=b2﹣4ac=(﹣2m)2﹣4×1×2(m+3)=4m2+8m+24=4(m+1)2+20,
∵无论m为何值时,4(m+1)2≥0, ∴△=4(m+1)2+20>0,
∴关于x的方程总有不相等的两个实数根,
即,无论m取何值,该函数总有两个零点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着科技的发展,某快递公司为了提高分拣包裹的速度,使用机器人代替人工进行包裹分拣,若甲机器人工作
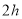 ,乙机器人工作
,乙机器人工作 ,一共可以分拣700件包裹;若甲机器人工作
,一共可以分拣700件包裹;若甲机器人工作 ,乙机器人工作
,乙机器人工作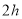 ,一共可以分拣650件包裹.
,一共可以分拣650件包裹.(1)求甲、乙两机器人每小时各分拣多少件包裹;
(2)去年“双十一”期间,快递公司的业务量猛增,为了让甲、乙两机器人每天分拣包裹的总数量不低于2250件,则它们每天至少要一起工作多少小时?
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图③所示,图象过点(﹣1,0),对称轴为直线x=2,则下 列结论中正确的个数有( )
①4a+b=0;
②9a+3b+c<0;
③若点A(﹣3,y1),点B(﹣
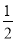 ,y2),点C(5,y3)在该函数图象上,则y1<y3<y2;
,y2),点C(5,y3)在该函数图象上,则y1<y3<y2;④若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2 , 且x1<x2 , 则x1<﹣1<5<x2 .
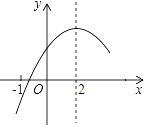
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在正方形
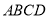 中,点
中,点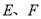 分别在
分别在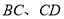 上,△
上,△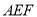 是等边三角形,连接
是等边三角形,连接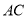 交
交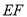 于
于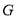 ,给出下列结论:
,给出下列结论: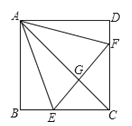
①
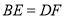 ; ②
; ② 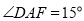 ;
;③
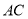 垂直平分
垂直平分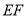 ; ④
; ④ .
.其中结论正确的共有( ).
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形
 中,
中,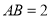 ,
,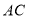 ,
,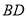 交于点
交于点 .若
.若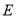 ,
,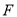 分别是边
分别是边 ,
,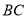 上的动点,且
上的动点,且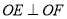 ,则
,则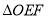 周长的最小值是__________.
周长的最小值是__________.
-
科目: 来源: 题型:
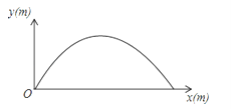
查看答案和解析>>【题目】如图,王强在一次高尔夫球的练习中,在某处击球,其飞行路线满足抛物线y=﹣
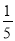 x2+
x2+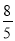 x,其中y(m)是球飞行的高度,x(m)是球飞行的水平距离.
x,其中y(m)是球飞行的高度,x(m)是球飞行的水平距离.(1)飞行的水平距离是多少时,球最高?
(2)球从飞出到落地的水平距离是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】为落实立德树人根本任务,培养德智体美劳全面发展的社会主义接班人,育才学校在设立学生奖学金时规定:每学期对学生的德智体美劳五个方面进行三次综合素质评价,分别是:假期综合素质评价、期中综合素质评价、期末综合素质评价,八年级(1)班的小明和八年级(2)班的小亮两位同学同时进入一等奖学金测评,他们的三次综合素质评价成绩如下表.
假期综合素质评价成绩
期中综合素质评价成绩
期末综合素质评价成绩
小明
96
91
92
小亮
95
93
91
(1)如果从三次综合素质评价成绩稳定性的角度来看,谁可以得一等奖学金?请你通过计算回答;
(2)如果假期综合素质评价成绩、期中综合素质评价成绩、期末综合素质评价成绩按
 的比例计入最终成绩,谁可以得一等奖学金?请你通过计算回答.
的比例计入最终成绩,谁可以得一等奖学金?请你通过计算回答.
相关试题

