【题目】菱形ABCD中,AB=4,∠ABC=60°,∠EAF的两边分别与射线CB、DC相交于点E、F,且∠EAF=60° 
(1)如图1,当点E是CB上任意一点时(点E不与B、C重合),求证:BE=CF;
(2)如图2,当点E在CB的延长线上时,且∠EAB=15°,求点F到BC的距离.
参考答案:
【答案】
(1)证明:连接AC,如图1中,∵∠BAC=∠EAF=60°,
∴∠BAE=∠CAE,
在△BAE和△CAF中,
 ,
,
∴△BAE≌△CAF,
∴BE=CF

(2)解:如图2中,过点A作AG⊥BC于点G,过点F作FH⊥EC于点H,
∵∠EAB=15°,∠ABC=60°,
∴∠AEB=45°,
在RT△AGB中,∵∠ABC=60°,AB=4,
∴BG= ![]() AB=2,AG=
AB=2,AG= ![]() BG=2
BG=2 ![]() ,
,
在RT△AEG中,∵∠AEG=∠EAG=45°,
∴AG=GE=2 ![]() ,
,
∴EB=EG﹣BG=2 ![]() ﹣2,
﹣2,
∵△AEB≌△AFC,
∴AE=AF,EB=CF=2 ![]() ﹣2,
﹣2,
在RT△CHF中,∵∠HCF=180°﹣∠BCD=60°,CF=2 ![]() ﹣2,
﹣2,
∴FH=CFsin60°=(2 ![]() ﹣2)
﹣2) ![]() =3﹣
=3﹣ ![]() .
.
∴点F到BC的距离为3﹣ ![]()

【解析】(1)欲证明BE=CF,只要证明△BAE≌△CAF即可.(2)过点A作AG⊥BC于点G,过点F作FH⊥EC于点H,根据FH=CFcos30°,因为CF=BE,只要求出BE即可解决问题.
【考点精析】解答此题的关键在于理解菱形的性质的相关知识,掌握菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半.
-
科目: 来源: 题型:
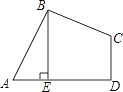
查看答案和解析>>【题目】如图,在四边形ABCD中,AB=BC,∠ABC=∠CDA=90°,BE⊥AD于点E,且四边形ABCD的面积为4,则BE等于________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的弦,过B作BC⊥AB交⊙O于C,过C作⊙O的切线,交AB的延长线于点D,E为AD的中点,过E作EF//BC交DC的延长线于点F,连接AF并延长BC的延长线于点G
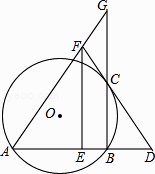
(1)求证:FC=FG;
(2)若BC=4,CG=6,求AB的长. -
科目: 来源: 题型:
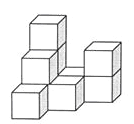
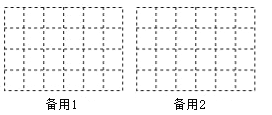
查看答案和解析>>【题目】下图是由几个相同的小正方体搭成的几何体,
(1)搭成这个几何体需要 个小正方体;
(2)画出这个几何体的主视图和左视图;
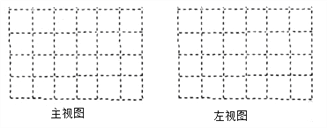
(3)在保持主视图和左视图不变的情况下,最多可以拿掉n个小正方体,则n= ,请在备用图中画出拿掉n个小正方体后新的几何体的俯视图.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)试验探索:
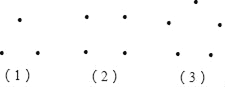
如果过每两点可以画一条直线,那么请下面三组图中分别画线,并回答问题:
第(1)组最多可以画______条直线;
第(2)组最多可以画______条直线;
第(3)组最多可以画______条直线.
(2)归纳结论:
如果平面上有n(n≥3)个点,且每3个点均不在一条直线上,那么最多可以画出直线______条.(作用含n的代数式表示)
(3)解决问题:
某班50名同学在毕业后的一次聚会中,若每两人握一次手问好,则共握 次手;最后,每两个人要互赠礼物留念,则共需 件礼物.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=ax2+bx+c与x轴交于A(1,0),B(3,0),与y轴交于C(0,﹣2),顶点为D,点E的坐标为(0,﹣1),该抛物线于BE交于另一点F,连接BC
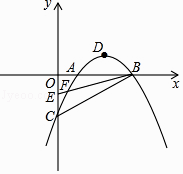
(1)求该抛物线的解析式;
(2)若点H(1,y)在BC上,连接FH,求△FHB的面积;
(3)一动点M从点D出发,以每秒1个单位的速度沿平行于y轴方向向上运动,连接OM,BM,设运动时间为t秒(t>0),点M在运动过程中,当t为何值时,∠OMB=90°?
(4)在x轴上方的抛物线上,是否存在点P,使得∠PBF被BA平分?若存在,直接写出点P的坐标;若不存在,请说明利由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是等腰直角三角形,∠A=90°,BC=4,点P是△ABC的边上一动点,沿B→A→C的路径移动,过点P作PD⊥BC于点D,设BD=x,△BDP的面积为y,则y与x函数关系的图象大致是( )

A.
B.
C.
D.
相关试题

