【题目】(1)试验探索:
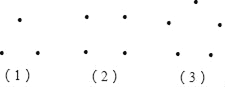
如果过每两点可以画一条直线,那么请下面三组图中分别画线,并回答问题:
第(1)组最多可以画______条直线;
第(2)组最多可以画______条直线;
第(3)组最多可以画______条直线.
(2)归纳结论:
如果平面上有n(n≥3)个点,且每3个点均不在一条直线上,那么最多可以画出直线______条.(作用含n的代数式表示)
(3)解决问题:
某班50名同学在毕业后的一次聚会中,若每两人握一次手问好,则共握 次手;最后,每两个人要互赠礼物留念,则共需 件礼物.
参考答案:
【答案】(1)见解析(2)![]() (3)1225;2450
(3)1225;2450
【解析】
(1)根据两点确定一条直线画出直线,观察后即可解答问题;
(2)根据上面得到的规律用代数式表示即可;
(3)将n=50代入可求得握手次数,送礼物时是双向的,因此是握手次数的2倍,由此即可求解.
(1)图形如下:
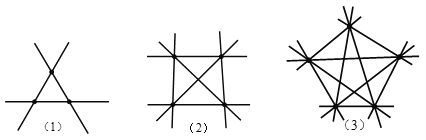
根据图形得:
第(1)组最多可以画3条直线;
第(2(组最多可以画6条直线;
第(3)组最多可以画10条直线;
(2)由(1)可知:
平面上有3个点时,最多可画直线1+2=3条,
平面上有4个点时,最多可画直线1+2+3=6条,
平面上有5个点时,最多可画直线1+2+3+4=10条,
……
所以平面上有n(n≥3)个点,且每3个点均不在1条直线上,那么最多可以画1+2+3+…+n-1=![]() 条直线,
条直线,
故答案为:![]() ;
;
(3)某班50名同学在毕业后的一次聚会中,若每两人握1次手问好,那么共握![]() =1225次手,
=1225次手,
互赠礼物为:1225×2=2450件,
故答案为:1225,2450.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的弦,过B作BC⊥AB交⊙O于C,过C作⊙O的切线,交AB的延长线于点D,E为AD的中点,过E作EF//BC交DC的延长线于点F,连接AF并延长BC的延长线于点G
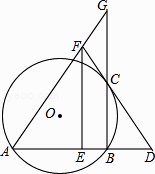
(1)求证:FC=FG;
(2)若BC=4,CG=6,求AB的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】下图是由几个相同的小正方体搭成的几何体,
(1)搭成这个几何体需要 个小正方体;
(2)画出这个几何体的主视图和左视图;
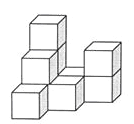
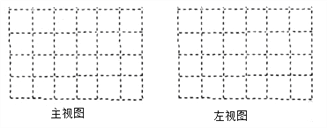
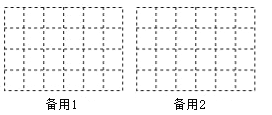
(3)在保持主视图和左视图不变的情况下,最多可以拿掉n个小正方体,则n= ,请在备用图中画出拿掉n个小正方体后新的几何体的俯视图.
-
科目: 来源: 题型:
查看答案和解析>>【题目】菱形ABCD中,AB=4,∠ABC=60°,∠EAF的两边分别与射线CB、DC相交于点E、F,且∠EAF=60°

(1)如图1,当点E是CB上任意一点时(点E不与B、C重合),求证:BE=CF;
(2)如图2,当点E在CB的延长线上时,且∠EAB=15°,求点F到BC的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=ax2+bx+c与x轴交于A(1,0),B(3,0),与y轴交于C(0,﹣2),顶点为D,点E的坐标为(0,﹣1),该抛物线于BE交于另一点F,连接BC
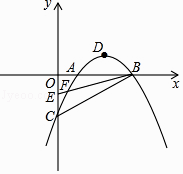
(1)求该抛物线的解析式;
(2)若点H(1,y)在BC上,连接FH,求△FHB的面积;
(3)一动点M从点D出发,以每秒1个单位的速度沿平行于y轴方向向上运动,连接OM,BM,设运动时间为t秒(t>0),点M在运动过程中,当t为何值时,∠OMB=90°?
(4)在x轴上方的抛物线上,是否存在点P,使得∠PBF被BA平分?若存在,直接写出点P的坐标;若不存在,请说明利由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是等腰直角三角形,∠A=90°,BC=4,点P是△ABC的边上一动点,沿B→A→C的路径移动,过点P作PD⊥BC于点D,设BD=x,△BDP的面积为y,则y与x函数关系的图象大致是( )

A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC和Rt△DCB中,AB=DC,∠A=∠D=90°,AC与BD交于点O,则有△________≌△________,其判定依据是________,还有△________≌△________,其判定依据是________.

相关试题

