搜索
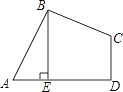
【题目】如图，在四边形ABCD中，AB=BC，∠ABC=∠CDA=90°，BE⊥AD于点E，且四边形ABCD的面积为4，则BE等于________．
参考答案：
【答案】2
【解析】
作BF⊥CD交DC的延长线于点F，根据条件可证得∠ABE=∠CBF，且由已知∠AEB=∠CFB=90°，AB=BC，所以△ABE≌△CBF，可得BE=BF；四边形ABCD的面积等于新正方形FBED的面积，即可得BE=2．
如图，过B作BF垂直DC的延长线于点F，
∵∠ABC=∠CDA=90°，BF⊥CD，
∴∠ABE+∠EBC=∠CBF+∠EBC，∴∠ABE=∠CBF，
又∵BE⊥AD，BF⊥DF，且AB=BC，
∴△ABE≌△CBF，即BE=BF，
∵BE⊥AD，∠CDA=90°，BE=BF，
∴四边形BEDF为正方形，
由以上得四边形ABCD的面积等于正方形BEDF的面积，即等于4，
∴BE=2，
故答案为：2.
-
科目： 来源： 题型：
查看答案和解析>>【题目】有理数a，b在数轴上的表示如图所示，则下列结论中： ①ab＜0， ②
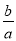＜0，③a+b＜0，④a-b＜0，⑤a＜|b|，⑥-a＞-b，正确的有（ ）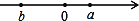
A. 2个 B. 3个 C. 4个 D. 5个
-
科目： 来源： 题型：
查看答案和解析>>【题目】为了了解某校九年级（1）班学生的体育测试情况，对全班学生的体育成绩进行了统计，并绘制出以下不完整的频数分布表和扇形统计图
分组
分数段（分）
频数
A
36≤x＜41
2
B
41≤x＜46
5
C
46≤x＜51
15
D
51≤x＜56
m
E
56≤x＜61
10
（1）求全班学生人数和m的值；
（2）该班学生的体育成绩的中位数落在哪个分数段内？
（3）该班体育成绩满分（60分）共有3人，其中男生2人，女生1人，现从这3人中随机选取2人参加校运动会，求恰好选到一男一女生的概率 -
科目： 来源： 题型：
查看答案和解析>>【题目】（1）阅读理解：
如图①，在△ABC中，若AB=10，AC=6，求BC边上的中线AD的取值范围．
解决此问题可以用如下方法：延长AD到点E使DE=AD，再连接BE（或将△ACD绕着点D逆时针旋转180°得到△EBD），把AB、AC，2AD集中在△ABE中，利用三角形三边的关系即可判断．
中线AD的取值范围是 ；
（2）问题解决：
如图②，在△ABC中，D是BC边上的中点，DE⊥DF于点D，DE交AB于点E，DF交AC于点F，连接EF，求证：BE+CF＞EF；
（3）问题拓展：
如图③，在四边形ABCD中，∠B+∠D=180°，CB=CD，∠BCD=140°，以为顶点作一个70°角，角的两边分别交AB，AD于E、F两点，连接EF，探索线段BE，DF，EF之间的数量关系，并加以证明．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，AB是⊙O的弦，过B作BC⊥AB交⊙O于C，过C作⊙O的切线，交AB的延长线于点D，E为AD的中点，过E作EF//BC交DC的延长线于点F，连接AF并延长BC的延长线于点G
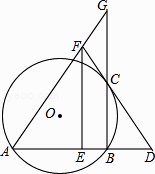
（1）求证：FC=FG；
（2）若BC=4，CG=6，求AB的长． -
科目： 来源： 题型：
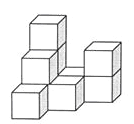
查看答案和解析>>【题目】下图是由几个相同的小正方体搭成的几何体，
（1）搭成这个几何体需要 个小正方体；
（2）画出这个几何体的主视图和左视图；
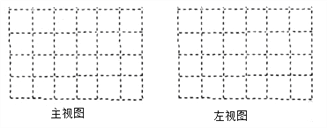
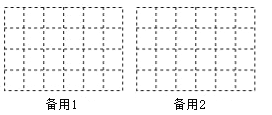
（3）在保持主视图和左视图不变的情况下，最多可以拿掉n个小正方体，则n= ，请在备用图中画出拿掉n个小正方体后新的几何体的俯视图.
-
科目： 来源： 题型：
查看答案和解析>>【题目】菱形ABCD中，AB=4，∠ABC=60°，∠EAF的两边分别与射线CB、DC相交于点E、F，且∠EAF=60°
（1）如图1，当点E是CB上任意一点时（点E不与B、C重合），求证：BE=CF；
（2）如图2，当点E在CB的延长线上时，且∠EAB=15°，求点F到BC的距离．
相关试题
