搜索
【题目】如图，△ABC是等腰直角三角形，∠A=90°，BC=4，点P是△ABC的边上一动点，沿B→A→C的路径移动，过点P作PD⊥BC于点D，设BD=x，△BDP的面积为y，则y与x函数关系的图象大致是（ ）
A.
B.
C.
D.
参考答案：
【答案】D
【解析】解：当点P在AB上时，△BDP是等腰直角三角形，故BD=x=DP，
∴△BDP的面积y= 
×BD×DP= x2 ， （0≤x≤2）
当点P在AC上时，△CDP是等腰直角三角形，BD=x，故CD=4﹣x=DP，
∴△BDP的面积y= ×BD×DP= x（4﹣x）=﹣ x2+2x，（2＜x≤4）
∴当0≤x≤2时，函数图象是开口向上的抛物线；
当2＜x≤4时，函数图象是开口向下的抛物线，
故选：D．
先根据点P在AB上时，得到△BDP的面积y= ×BD×DP= x2 ， （0≤x≤2），再根据点P在AC上时，△BDP的面积y= ×BD×DP=﹣ x2+2x，（2＜x≤4），进而得到y与x函数关系的图象．
-
科目： 来源： 题型：
查看答案和解析>>【题目】菱形ABCD中，AB=4，∠ABC=60°，∠EAF的两边分别与射线CB、DC相交于点E、F，且∠EAF=60°
（1）如图1，当点E是CB上任意一点时（点E不与B、C重合），求证：BE=CF；
（2）如图2，当点E在CB的延长线上时，且∠EAB=15°，求点F到BC的距离． -
科目： 来源： 题型：
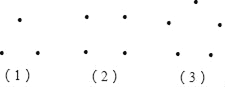
查看答案和解析>>【题目】（1）试验探索：
如果过每两点可以画一条直线，那么请下面三组图中分别画线，并回答问题：
第（1）组最多可以画______条直线；
第（2）组最多可以画______条直线；
第（3）组最多可以画______条直线．
（2）归纳结论：
如果平面上有n（n≥3）个点，且每3个点均不在一条直线上，那么最多可以画出直线______条．（作用含n的代数式表示）
（3）解决问题：
某班50名同学在毕业后的一次聚会中，若每两人握一次手问好，则共握 次手；最后，每两个人要互赠礼物留念，则共需 件礼物．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知抛物线y=ax2+bx+c与x轴交于A（1，0），B（3，0），与y轴交于C（0，﹣2），顶点为D，点E的坐标为（0，﹣1），该抛物线于BE交于另一点F，连接BC
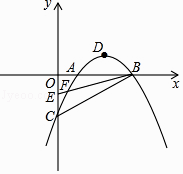
（1）求该抛物线的解析式；
（2）若点H（1，y）在BC上，连接FH，求△FHB的面积；
（3）一动点M从点D出发，以每秒1个单位的速度沿平行于y轴方向向上运动，连接OM，BM，设运动时间为t秒（t＞0），点M在运动过程中，当t为何值时，∠OMB=90°？
（4）在x轴上方的抛物线上，是否存在点P，使得∠PBF被BA平分？若存在，直接写出点P的坐标；若不存在，请说明利由． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在Rt△ABC和Rt△DCB中，AB=DC，∠A=∠D=90°，AC与BD交于点O，则有△________≌△________，其判定依据是________，还有△________≌△________，其判定依据是________．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，AB是半圆直径，半径OC⊥AB于点O，AD平分∠CAB交弧
于点D，连接CD、OD．下列结论：①AC∥OD；②CE=OE；③∠OED=∠AOD；④CD=DE．其中正确结论的个数有（ ） 
A.1个
B.2个
C.3个
D.4个 -
科目： 来源： 题型：
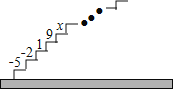
查看答案和解析>>【题目】如图，阶梯图的每个台阶上都标着一个数，从下到上的第1个至第4个台阶上依次标着﹣5，﹣2，1，9，且任意相邻四个台阶上数的和都相等．
尝试 （1）求前4个台阶上数的和是多少？
（2）求第5个台阶上的数x是多少？
应用 求从下到上前31个台阶上数的和．
发现 试用含k（k为正整数）的式子表示出数“1”所在的台阶数．
相关试题
