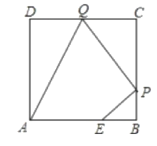
【题目】如图,已知正方形ABCD边长为3,点E在AB边上且BE=1,点P,Q分别是边BC,CD的动点(均不与顶点重合),当四边形AEPQ的周长取最小值时,四边形AEPQ的面积是___.
参考答案:
【答案】![]()
【解析】
根据最短路径的求法,先确定点E关于BC的对称点E′,再确定点A关于DC的对称点A′,连接A′E′即可得出P,Q的位置;再根据相似得出相应的线段长从而可求得四边形AEPQ的面积.
如图所示:
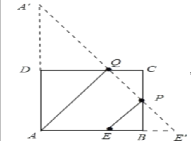
作E关于BC的对称点E′,点A关于DC的对称点A′,连接A′E′,四边形AEPQ的周长最小,
∵AD=A′D=3,BE=BE′=1,
∴AA′=6,AE′=4.
∵DQ∥AE′,D是AA′的中点,
∴DQ是△AA′E′的中位线,
∴DQ=![]() AE′=2;CQ=DCCQ=32=1,
AE′=2;CQ=DCCQ=32=1,
∵BP∥AA′,
∴△BE′P∽△AE′A′,
∴![]() ,
,
即![]() ,
,
解得:BP=1.5,
∴CP=BCBP=31.5=1.5,
S四边形AEPQ=S正方形ABCDS△ADQS△PCQS△BEP=9![]() ADDQ
ADDQ![]() CQCP
CQCP![]() BEBP=
BEBP=
=9![]() ×3×2
×3×2![]() ×1×
×1×![]()
![]() ×1×
×1×![]() =
=![]() ,
,
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系中,对于点
 和点
和点 ,给出如下定义:
,给出如下定义:若
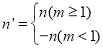 则称点
则称点 为点
为点 的可变点.例如:点
的可变点.例如:点 的可变点的坐标是
的可变点的坐标是  ,点
,点 的可变点的坐标是
的可变点的坐标是  .
. (1)①点
 的可变点的坐标是 ;
的可变点的坐标是 ;②在点
 ,
, 中有一个点是函数
中有一个点是函数 图象上某一个点的可变点,这个点是 ;(填“A”或“B”)
图象上某一个点的可变点,这个点是 ;(填“A”或“B”)(2)若点
 在函数
在函数  的图象上,求其可变点
的图象上,求其可变点 的纵坐标
的纵坐标 的取值范围;
的取值范围;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个自然数可以表示为三个连续奇数的和,那么我们就称这个数为“锦鲤数”,如:9=1+3+5,所以9是“锦鲤数”.
(1)请问21和35是不是“锦鲤数”,并说明理由;
(2)规定:
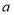
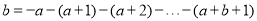 (其中
(其中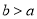 ,且
,且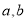 为自然数),是否存在一个“锦鲤数”
为自然数),是否存在一个“锦鲤数”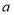 ,使得
,使得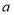 50=-3666.若存在,则求出
50=-3666.若存在,则求出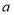 ,并把
,并把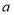 表示成3个连续的奇数和的形式,若不存在,请说明理由.
表示成3个连续的奇数和的形式,若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】一只不透明的袋子中装有4个小球,分别标有数字2,3,4,
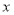 ,这些球除数字外都相同.甲、乙两人每次同时从袋中各随机摸出1个球,并计算摸出的这2个小球上数字之和.记录后都将小球放回袋中搅匀,进行重复实验.实验数据如下表:
,这些球除数字外都相同.甲、乙两人每次同时从袋中各随机摸出1个球,并计算摸出的这2个小球上数字之和.记录后都将小球放回袋中搅匀,进行重复实验.实验数据如下表:摸球总次数
10
20
30
60
90
120
180
240
330
450
“和为7”出现的频数
1
9
14
24
26
37
58
82
109
150
“和为7”出现的频率
0.10
0.45
0.47
0.40
0.29
0.31
0.32
0.34
0.33
0.33
试估计出现“和为7”的概率为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AD=5,CD=3,∠ABC=∠ACB=∠ADC=45°,则BD的长为()

A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:AB是⊙0直径,C是⊙0外一点,连接BC交⊙0于点D,BD=CD,连接AD、AC.
(1)如图1,求证:∠BAD=∠CAD
(2)如图2,过点C作CF⊥AB于点F,交⊙0于点E,延长CF交⊙0于点G.过点作EH⊥AG于点H,交AB于点K,求证AK=2OF;
(3)如图3,在(2)的条件下,EH交AD于点L,若0K=1,AC=CG,求线段AL的长.

图1 图2 图3
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数轴上点A表示数
 ,点B表示数
,点B表示数 ,AB表示点A和点B之间的距离.
,AB表示点A和点B之间的距离. ,
, 满足
满足 .
.(1)在原点O处放了一挡板,若一小球P从点A处以3个单位/秒的速度向左运动,同时另一个小球Q从点B处以4个单位/秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看作一点)以原来的速度向相反方向运动,设运动时间t(秒),问t为何值时,P、Q两球到原点的距离相等?
(2)若小球P从点A以每秒4个单位的速度向右运动,小球Q同时从点B以每秒3个单位得速度向左运动,则是否存在时间t,使得AP+BQ=2PQ?若存在,请求出时间t;若不存在,请说明理由.
相关试题

