【题目】在数轴上点A表示数![]() ,点B表示数
,点B表示数![]() ,AB表示点A和点B之间的距离.
,AB表示点A和点B之间的距离.![]() ,
,![]() 满足
满足![]() .
.
(1)在原点O处放了一挡板,若一小球P从点A处以3个单位/秒的速度向左运动,同时另一个小球Q从点B处以4个单位/秒的速度也向左运动,在碰到挡板后(忽略球的大小,可看作一点)以原来的速度向相反方向运动,设运动时间t(秒),问t为何值时,P、Q两球到原点的距离相等?
(2)若小球P从点A以每秒4个单位的速度向右运动,小球Q同时从点B以每秒3个单位得速度向左运动,则是否存在时间t,使得AP+BQ=2PQ?若存在,请求出时间t;若不存在,请说明理由.
参考答案:
【答案】(1)1,15;(2)否,理由见解析
【解析】
(1)先根据绝对值和完全平方的非负性得出![]() ,
,![]() 的值,再根据题意列出方程即可求解;
的值,再根据题意列出方程即可求解;
(2)先根据题意列出AP、BQ、PQ的代数式,再列出方程求解即可.
(1)由题意得:![]() ,
,![]()
解得:![]() ,
,![]()
∴![]() ,
,![]()
∴![]() ,
,![]()
根据题意得:![]()
∴当![]() 时,
时,![]() ,解得:
,解得:![]()
当![]() 时,
时,![]() ,解得:
,解得:![]() ;
;
(2)①当P在OA之间且未碰到挡板时,![]() ,
,
AP=4t,QB=3t,PQ=15-4t-3t=15-7t
∴4t+3t=2(15-7t)
解得:![]() (舍去);
(舍去);
②当P碰到挡板反弹后在OA之间时,![]() ,
,
AP=8-4t,QB=3t,PQ=11-3t+4t-4=t+7
∴8-4t+3t=2(t+7)
解得:t=-2(舍去)
③当P碰到挡板反弹后过了A点,且Q还未碰到挡板时,![]()
AP=4t-8,QB=3t,PQ=11-3t+4t-4=t+7
∴4t-8+3t=2(t+7)
解得:![]() (舍去);
(舍去);
④当Q碰到挡板反弹后在OB之间时,![]()
AP=4t-8,QB=22-3t,PQ=3t-11+4t-4=7t-15
∴4t-8+22-3t=2(7t-15)
解得:![]() (舍去);
(舍去);
⑤当Q碰到挡板反弹后过了B点时,![]()
AP=4t-8,QB=3t-22,PQ=3t-11+4t-4=7t-15
∴4t-8+3t-22=2(7t-15)该方程无解
综上所述:不存在时间t,使得AP+BQ=2PQ.
-
科目: 来源: 题型:
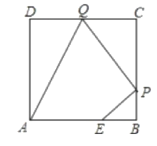
查看答案和解析>>【题目】如图,已知正方形ABCD边长为3,点E在AB边上且BE=1,点P,Q分别是边BC,CD的动点(均不与顶点重合),当四边形AEPQ的周长取最小值时,四边形AEPQ的面积是___.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AD=5,CD=3,∠ABC=∠ACB=∠ADC=45°,则BD的长为()

A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:AB是⊙0直径,C是⊙0外一点,连接BC交⊙0于点D,BD=CD,连接AD、AC.
(1)如图1,求证:∠BAD=∠CAD
(2)如图2,过点C作CF⊥AB于点F,交⊙0于点E,延长CF交⊙0于点G.过点作EH⊥AG于点H,交AB于点K,求证AK=2OF;
(3)如图3,在(2)的条件下,EH交AD于点L,若0K=1,AC=CG,求线段AL的长.

图1 图2 图3
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校随机抽取本校部分同学,调查同学了解母亲生日日期的情况,分“知道、不知道、记不清”三种.下面图①、图②是根据采集到的数据,绘制的扇形和条形统计图.

请你要根据图中提供的信息,解答下列问题:
(1)求本次被调查学生的人数,并补全条形统计图;
(2)在图①中,求出“不知道”部分所对应的圆心角的度数;
(3)若全校共有1440名学生,请你估计这所学校有多少名学生知道母亲的生日?
-
科目: 来源: 题型:
查看答案和解析>>【题目】若实数m,n,p满足m<n<p(mp<0)且|p|<|n|<|m|,则|x﹣m|+|x+n|+|x+p|的最小值是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,O为坐标原点,抛物线
 交x轴于点A(l,0)、B(3,0),交y轴于点C.
交x轴于点A(l,0)、B(3,0),交y轴于点C.(1)如图1,求抛物线的解析式;
(2)如图2,点P为对称轴右侧第四象限抛物线上一点,连接PA并延长交y轴于点K,点P横坐标为t,△PCK的面积为S,求S与t的函数关系式(直接写出自变量t的取值范围);
(3)如图3,在(2)的条件下,过点A作AD⊥AP交y轴于点D.连接OP,过点O作OE⊥OP交AD延长线于点E,当OE=OP时,延长EA交抛物线于点Q,点M在直线EC上,连接QM,交AB于点H,将射线QM绕点Q逆时针旋转45°,得到射线QN交AB于点F,交直线EC于点N,若AH:HF=3:5,求
 的值.
的值.
相关试题

