【题目】一只不透明的袋子中装有4个小球,分别标有数字2,3,4,![]() ,这些球除数字外都相同.甲、乙两人每次同时从袋中各随机摸出1个球,并计算摸出的这2个小球上数字之和.记录后都将小球放回袋中搅匀,进行重复实验.实验数据如下表:
,这些球除数字外都相同.甲、乙两人每次同时从袋中各随机摸出1个球,并计算摸出的这2个小球上数字之和.记录后都将小球放回袋中搅匀,进行重复实验.实验数据如下表:
摸球总次数 | 10 | 20 | 30 | 60 | 90 | 120 | 180 | 240 | 330 | 450 |
“和为7”出现的频数 | 1 | 9 | 14 | 24 | 26 | 37 | 58 | 82 | 109 | 150 |
“和为7”出现的频率 | 0.10 | 0.45 | 0.47 | 0.40 | 0.29 | 0.31 | 0.32 | 0.34 | 0.33 | 0.33 |
试估计出现“和为7”的概率为________.
参考答案:
【答案】0.33
【解析】
由于大量试验中“和为7”出现的频数稳定在0.3附近,据图表,可估计“和为7”出现的概率为3.1,3.2,3.3等均可.
出现和为7的概率是:0.33(或0.31,0.32,0.34均正确);
故答案为:0.33
-
科目: 来源: 题型:
查看答案和解析>>【题目】某中学为了进一步了解八年级学生的身体素质情况,由体育老师随机抽取了八年级
 名学生进行一分钟跳绳测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图.如下所示:
名学生进行一分钟跳绳测试,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图.如下所示:

请结合图表完成下列问题:
(1)表中的
 ,
, ;
;(2)请把频数分布直方图补充完整;
(3)若八年级学生一分钟跳绳的成绩标准是:

 为不合格;
为不合格; 为合格;
为合格; 为良好;
为良好;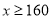 为优秀.如果该年级有
为优秀.如果该年级有 名学生,根据以上信息,请你估计该年级跳绳不合格的人数为 ;优秀的人数为 .
名学生,根据以上信息,请你估计该年级跳绳不合格的人数为 ;优秀的人数为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系中,对于点
 和点
和点 ,给出如下定义:
,给出如下定义:若
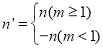 则称点
则称点 为点
为点 的可变点.例如:点
的可变点.例如:点 的可变点的坐标是
的可变点的坐标是  ,点
,点 的可变点的坐标是
的可变点的坐标是  .
. (1)①点
 的可变点的坐标是 ;
的可变点的坐标是 ;②在点
 ,
, 中有一个点是函数
中有一个点是函数 图象上某一个点的可变点,这个点是 ;(填“A”或“B”)
图象上某一个点的可变点,这个点是 ;(填“A”或“B”)(2)若点
 在函数
在函数  的图象上,求其可变点
的图象上,求其可变点 的纵坐标
的纵坐标 的取值范围;
的取值范围;
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个自然数可以表示为三个连续奇数的和,那么我们就称这个数为“锦鲤数”,如:9=1+3+5,所以9是“锦鲤数”.
(1)请问21和35是不是“锦鲤数”,并说明理由;
(2)规定:
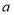
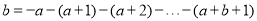 (其中
(其中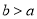 ,且
,且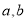 为自然数),是否存在一个“锦鲤数”
为自然数),是否存在一个“锦鲤数”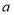 ,使得
,使得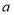 50=-3666.若存在,则求出
50=-3666.若存在,则求出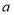 ,并把
,并把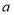 表示成3个连续的奇数和的形式,若不存在,请说明理由.
表示成3个连续的奇数和的形式,若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知正方形ABCD边长为3,点E在AB边上且BE=1,点P,Q分别是边BC,CD的动点(均不与顶点重合),当四边形AEPQ的周长取最小值时,四边形AEPQ的面积是___.
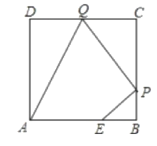
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AD=5,CD=3,∠ABC=∠ACB=∠ADC=45°,则BD的长为()

A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:AB是⊙0直径,C是⊙0外一点,连接BC交⊙0于点D,BD=CD,连接AD、AC.
(1)如图1,求证:∠BAD=∠CAD
(2)如图2,过点C作CF⊥AB于点F,交⊙0于点E,延长CF交⊙0于点G.过点作EH⊥AG于点H,交AB于点K,求证AK=2OF;
(3)如图3,在(2)的条件下,EH交AD于点L,若0K=1,AC=CG,求线段AL的长.

图1 图2 图3
相关试题

