【题目】下列各数: ![]() ,3.1415,
,3.1415, ![]() ,0,
,0, ![]() ,
, ![]() ,1.3030030003……(每两个3之间多一个0)中,
,1.3030030003……(每两个3之间多一个0)中,
(1)无理数为:;
(2)整数为:;
(3)按从小到大排列,并用“<”连接.
参考答案:
【答案】
(1)![]() ,1.3030030003……(每两个3之间多一个0)
,1.3030030003……(每两个3之间多一个0)
(2)![]() ,0,
,0,![]()
(3)解: ![]()
【解析】(1)无限不循环的小数就是无理数,有限小数和无限循环小数就是有理数,根据有理数和无理数的定义判断即可;
(2)正数包括正整数,负整数和零三部分,判断之前应该先把含有运算符号的进行化简;
(3)按照正数大于零,零大于负数,两个负数比大小绝对值大的反而小,进行比较排序即可。
【考点精析】解答此题的关键在于理解无理数的相关知识,掌握在理解无理数时,要抓住“无限不循环”这个要点,归纳起来有四类:(1)开方开不尽的数;(2)有特定意义的数,如圆周率π,或化简后含有π的数;(3)有特定结构的数,如0.1010010001…等;(4)某些三角函数,如sin60o等,以及对实数的大小比较的理解,了解数轴比较;求差比较;求商比较法;绝对值比较法;平方法.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有16筐白菜,以每筐30千克为标准,超过或不足的分别用正、负来表示,记录如下:

(1)16筐白菜中,最重的一筐比最轻的一筐要重多少千克?
(2)与标准质量比较,16筐白菜总计超过或不足多少千克?
(3)若白菜每千克售价3元,则出售这16筐白菜可卖多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】从2开始,连续的偶数相加,它们和的情况如下表:

(1)如果n =8时,那么S的值为;
(2)根据表中的规律猜想:用n的代数式表示S的公式为S=2+4+6+8+…+2n =;
(3)根据上题的规律计算102+104+106+…+2006的值(要有计算过程). -
科目: 来源: 题型:
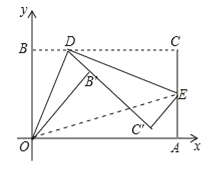
查看答案和解析>>【题目】如图,将矩形纸片ABCD置于直角坐标系中,点A(4,0),点B(0,3),点D(异于点B、C)为边BC上动点,过点O、D折叠纸片,得点B′和折痕OD.过点D再次折叠纸片,使点C落在直线DB′上,得点C′和折痕DE,连接OE,设BD=t.
(1)当t=1时,求点E的坐标;
(2)设S四边形OECB=s,用含t的式子表示s(要求写出t的取值范围);
(3)当OE取最小值时,求点E的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的一元二次方程x(x+2)=m总有两个不相等的实数根,则m的取值范围是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小聪是个数学爱好者,他发现从1开始,连续几个奇数相加,和的变化规律如右表所示:
加数个数
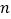
连续奇数的和S
1
1=
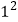
2
1+3=22
3
1+3+5=32
4
1+3+5+7=42
5
1+3+5+7+9=52
n
…
(1)如果n=7,则S的值为;
(2)求1+3+5+7+…+199的值;
(3)求13+15+17+…+79的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】若y轴上的点P到x轴的距离为3,则点P的坐标是( )
A.(3,0)
B.(0,3)
C.(3,0)或(﹣3,0)
D.(0,3)或(0,﹣3)
相关试题

