【题目】小聪是个数学爱好者,他发现从1开始,连续几个奇数相加,和的变化规律如右表所示:
加数个数 | 连续奇数的和S |
1 | 1= |
2 | 1+3=22 |
3 | 1+3+5=32 |
4 | 1+3+5+7=42 |
5 | 1+3+5+7+9=52 |
n | … |
(1)如果n=7,则S的值为;
(2)求1+3+5+7+…+199的值;
(3)求13+15+17+…+79的值.
参考答案:
【答案】
(1)解:1+3+5+7+9+11+13=72=49;
(2)解:∵(199+1)÷2=100,
∴1+3+5+7+…+199=1002=10000.
(3)解:∵1+3+5+…+11+13+15+17+…+79=402,
1+3+5+…+11=62,
∴13+15+17+…+79=402-62=1564
【解析】(1)观察表格发现连续几个奇数相加其和=加数的个数的平方,根据规律计算即可;
(2)首先用这组连续奇数的首加尾的和除以2得出加数的个数,然后利用连续几个奇数相加其和=加数的个数的平方计算出结果即可;
(3)首先利用(1)小题找到的规律计算出1+3+5+…+11+13+15+17+…+79的结果,然后再利用规律计算出1+3+5+…+11的和,最后用1+3+5+…+11+13+15+17+…+79的结果-1+3+5+…+11的和即可。
【考点精析】掌握数与式的规律是解答本题的根本,需要知道先从图形上寻找规律,然后验证规律,应用规律,即数形结合寻找规律.
-
科目: 来源: 题型:
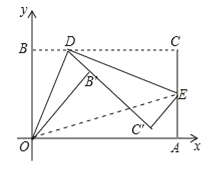
查看答案和解析>>【题目】如图,将矩形纸片ABCD置于直角坐标系中,点A(4,0),点B(0,3),点D(异于点B、C)为边BC上动点,过点O、D折叠纸片,得点B′和折痕OD.过点D再次折叠纸片,使点C落在直线DB′上,得点C′和折痕DE,连接OE,设BD=t.
(1)当t=1时,求点E的坐标;
(2)设S四边形OECB=s,用含t的式子表示s(要求写出t的取值范围);
(3)当OE取最小值时,求点E的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各数:
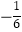 ,3.1415,
,3.1415, 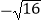 ,0,
,0, 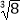 ,
,  ,1.3030030003……(每两个3之间多一个0)中,
,1.3030030003……(每两个3之间多一个0)中,
(1)无理数为:;
(2)整数为:;
(3)按从小到大排列,并用“<”连接. -
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的一元二次方程x(x+2)=m总有两个不相等的实数根,则m的取值范围是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若y轴上的点P到x轴的距离为3,则点P的坐标是( )
A.(3,0)
B.(0,3)
C.(3,0)或(﹣3,0)
D.(0,3)或(0,﹣3) -
科目: 来源: 题型:
查看答案和解析>>【题目】如果∠α=30°,那么∠α的余角是( )
A.30°
B.150°
C.60°
D.70° -
科目: 来源: 题型:
查看答案和解析>>【题目】目前节能灯在各城市已基本普及,今年某市面向县级及农村地区推广,为响应号召,朝阳灯饰商场用了4200元购进甲型和乙型两种节能灯.这两种型号节能灯的进价、售价如表:
进价(元/只)
售价(元/只)
甲型
25
30
乙型
45
60
特别说明:毛利润=售价﹣进价
(1)朝阳灯饰商场销售甲型节能灯一只毛利润是元;
(2)朝阳灯饰商场购买甲,乙两种节能灯共100只,其中买了甲型节能灯多少只?
(3)现在朝阳灯饰商场购进甲型节能灯m只,销售完节能灯时所获的毛利润为1080元.求m的值.
相关试题

