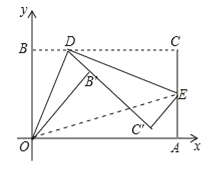
【题目】如图,将矩形纸片ABCD置于直角坐标系中,点A(4,0),点B(0,3),点D(异于点B、C)为边BC上动点,过点O、D折叠纸片,得点B′和折痕OD.过点D再次折叠纸片,使点C落在直线DB′上,得点C′和折痕DE,连接OE,设BD=t.
(1)当t=1时,求点E的坐标;
(2)设S四边形OECB=s,用含t的式子表示s(要求写出t的取值范围);
(3)当OE取最小值时,求点E的坐标.
参考答案:
【答案】(1)(4,2);(2)S=![]() (0<t<4);(3)(4,
(0<t<4);(3)(4,![]() ).
).
【解析】
试题分析:(1)根据折叠的性质和全等三角形的判定定理证明△BOD≌△CDE,求出CE,计算出AE,得到点E的坐标;
(2)根据相似三角形的性质用t表示出CE,根据梯形的面积公式用t表示S;
(3)根据二次函数的性质求出AE的最小值,求出点E的坐标.
试题解析:(1)由折叠的性质可知,∠ODB=∠ODB′,∠EDC=∠EDC′,∴∠ODE=90°,∴∠BDO+∠CDE=90°,又∠BDO+∠BOD=90°,∴∠BOD=∠CDE,∵BD=t=1,BC=4,∴CD=3,又OB=3,∴OB=CD,在△BOD和△CDE中,∵∠B=∠C,OB=CD,∠BOD=∠CDE,∴△BOD≌△CDE,∴CE=BD=1,∴AE=AC﹣CE=2,∴点E的坐标为(4,2);
(2)∵BD=t,∴DC=BC﹣BD=4﹣t,由(1)得,∠BOD=∠CDE,又∠B=∠C=90°,∴△ODB∽△DCE,∴![]() ,即
,即![]() ,解得,CE=
,解得,CE=![]() ,∴S=
,∴S=![]() ×(CE+OB)×BC=
×(CE+OB)×BC=![]() ×(
×(![]() +3)×4,∴S=
+3)×4,∴S=![]() (0<t<4);
(0<t<4);
(3)在Rt△OEA中,OE2=OA2+AE2=42+AE2,∴当AE最小时,OE最小,由(2)得,CE=![]() ,∴AE=AC﹣CE=
,∴AE=AC﹣CE=![]() =
=![]() ,当t=2时,AE的最小值为
,当t=2时,AE的最小值为![]() ,此时点E的坐标为(4,
,此时点E的坐标为(4,![]() ).
).
-
科目: 来源: 题型:
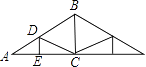
查看答案和解析>>【题目】如图是屋架设计图的一部分,点D是斜梁AB的中点,立柱BC、DE垂直于横梁AC,AB=8m,∠A=30°,则DE=m.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有16筐白菜,以每筐30千克为标准,超过或不足的分别用正、负来表示,记录如下:

(1)16筐白菜中,最重的一筐比最轻的一筐要重多少千克?
(2)与标准质量比较,16筐白菜总计超过或不足多少千克?
(3)若白菜每千克售价3元,则出售这16筐白菜可卖多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】从2开始,连续的偶数相加,它们和的情况如下表:

(1)如果n =8时,那么S的值为;
(2)根据表中的规律猜想:用n的代数式表示S的公式为S=2+4+6+8+…+2n =;
(3)根据上题的规律计算102+104+106+…+2006的值(要有计算过程). -
科目: 来源: 题型:
查看答案和解析>>【题目】下列各数:
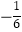 ,3.1415,
,3.1415, 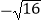 ,0,
,0, 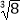 ,
,  ,1.3030030003……(每两个3之间多一个0)中,
,1.3030030003……(每两个3之间多一个0)中,
(1)无理数为:;
(2)整数为:;
(3)按从小到大排列,并用“<”连接. -
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的一元二次方程x(x+2)=m总有两个不相等的实数根,则m的取值范围是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小聪是个数学爱好者,他发现从1开始,连续几个奇数相加,和的变化规律如右表所示:
加数个数
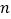
连续奇数的和S
1
1=
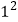
2
1+3=22
3
1+3+5=32
4
1+3+5+7=42
5
1+3+5+7+9=52
n
…
(1)如果n=7,则S的值为;
(2)求1+3+5+7+…+199的值;
(3)求13+15+17+…+79的值.
相关试题

