【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() 点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动,设点D、E运动的时间是t秒
点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动,设点D、E运动的时间是t秒![]() 过点D作
过点D作![]() 于点F,连接DE、EF.
于点F,连接DE、EF.
![]() 求证:
求证:![]() ;
;
![]() 四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由.
四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由.
![]() 当t为何值时,
当t为何值时,![]() 为直角三角形?请说明理由.
为直角三角形?请说明理由.

参考答案:
【答案】(1)证明见解析;(2)能,理由见解析;(3)![]() 秒或4秒时,
秒或4秒时,![]() 为直角三角形.
为直角三角形.
【解析】
![]() 在
在![]() 中,
中,![]() ,
,![]() ,根据30°角直角三角形的性质及已知条件即可证得结论;
,根据30°角直角三角形的性质及已知条件即可证得结论;![]() 先证得四边形AEFD为平行四边形,使AEFD为菱形则需要满足的条件为AE=AD,由此即可解答;
先证得四边形AEFD为平行四边形,使AEFD为菱形则需要满足的条件为AE=AD,由此即可解答;![]() 时,四边形EBFD为矩形
时,四边形EBFD为矩形![]() 在Rt△AED中求可得
在Rt△AED中求可得![]() ,由此即可解答;
,由此即可解答;![]() 时,由
时,由![]() 知
知![]() ,则得
,则得![]() ,求得
,求得![]() ,由此列方程求解即可;
,由此列方程求解即可;![]() 时,此种情况不存在.
时,此种情况不存在.
![]() 证明:在
证明:在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
![]() .
.
又![]() ,
,
![]() .
.
![]() 解:能
解:能![]() 理由如下:
理由如下:
![]() ,
,![]() ,
,
![]() .
.
又![]() ,
,
![]() 四边形AEFD为平行四边形.
四边形AEFD为平行四边形.
![]() ,
,
![]() .
.
![]() .
.
若使AEFD为菱形,则需![]() ,
,
即![]() ,
,![]() .
.
即当![]() 时,四边形AEFD为菱形.
时,四边形AEFD为菱形.
![]() 解:
解:![]() 时,四边形EBFD为矩形.
时,四边形EBFD为矩形.
在![]() 中,
中,![]() ,
,
![]() .
.
即![]() ,
,![]() .
.
![]() 时,由
时,由![]() 四边形AEFD为平行四边形知
四边形AEFD为平行四边形知![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
即![]() ,
,![]() .
.
![]() 时,此种情况不存在.
时,此种情况不存在.
综上所述,当![]() 秒或4秒时,
秒或4秒时,![]() 为直角三角形.
为直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(8 分)2013 年 4 月起泉州市区居民生活用水开始实行阶梯式计量水价,据了解,此次实行的阶梯式计量水价分为三级(如表所示):

例:若某用户 2013 年 6 月份的用水量为 35 吨,按三级计算则应交水费为:
20×1.65+(30﹣20)×2.48+(35﹣30)×3.30=74.3(元)
(1)如果小东家 2013 年 6 月份的用水量为 20 吨,则需缴交水费多少元?
(2)如果小明家 2013 年 7 月份的用水量为 a 吨,水价要按两级计算,则小明家该月应缴交水费多少元?(用含 a 的代数式表示,并化简)
(3)若一用户 2013 年 7 月份应该水费 90.8 元,则该户人家 7 月份用水多少吨?
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC在平面直角坐标系xOy中的位置如图所示.

(1)作△ABC关于点C成中心对称的△A1B1C1.
(2)将△A1B1C1向右平移4个单位,作出平移后的△A2B2C2.
(3)在x轴上求作一点P,使PA1+PC2的值最小,并写出点P的坐标(不写解答过程,直接写出结果)
-
科目: 来源: 题型:
查看答案和解析>>【题目】“汉十”高速铁路襄阳段正在建设中,甲、乙两个工程队计划参与一项工程建设,甲队单独施工30天完成该项工程的
 ,这时乙队加入,两队还需同时施工15天,才能完成该项工程.
,这时乙队加入,两队还需同时施工15天,才能完成该项工程.
(1)若乙队单独施工,需要多少天才能完成该项工程?
(2)若甲队参与该项工程施工的时间不超过36天,则乙队至少施工多少天才能完成该项工程? -
科目: 来源: 题型:
查看答案和解析>>【题目】有理数 a、b、c 在数轴上的位置如图所示:
(1)比较 a、|b|、c 的大小(用“<”连接);
(2)若 m=|a+b|﹣|b﹣1|﹣|a﹣c|,求 1﹣2013(m+c)2013 的值;
(3)若 a=﹣2,b=﹣3,c=
 ,且 a、b、c 对应的点分别为 A、B、C,问在数轴上是否存在一点 P,使 P 与 A 的距离是 P 与 C 的距离的 3 倍?若存在,请求出 P 点对应的有理数;若不存在,请说明理由.
,且 a、b、c 对应的点分别为 A、B、C,问在数轴上是否存在一点 P,使 P 与 A 的距离是 P 与 C 的距离的 3 倍?若存在,请求出 P 点对应的有理数;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB经过⊙O上的点C,直线AO与⊙O交于点E和点D,OB与⊙O交于点F,连接DF、DC.已知OA=OB,CA=CB,DE=10,DF=6.
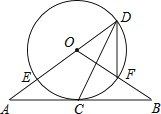
(1)求证:①直线AB是⊙O的切线;②∠FDC=∠EDC;
(2)求CD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读下面的村料,再分解因式.
要把多项式
 分解因式,可以先把它的前两项分成组,并提出a,把它的后两项分成组,并提出b,从而得
分解因式,可以先把它的前两项分成组,并提出a,把它的后两项分成组,并提出b,从而得 .
.这时,由于
 中又有公困式
中又有公困式 ,于是可提公因式
,于是可提公因式 ,从而得到
,从而得到 ,因此有
,因此有


 .
.这种因式分解的方法叫做分组分解法,如果把一个多项式各个项分组并提出公因式后,它们的另一个因式正好相同,那么这个多项式就可以利用分组分解法来因式分解.
请用上面材料中提供的方法因式分解:

 请你完成分解因式下面的过程
请你完成分解因式下面的过程
 ______
______ ;
; .
.
相关试题

