【题目】有理数 a、b、c 在数轴上的位置如图所示:
(1)比较 a、|b|、c 的大小(用“<”连接);
(2)若 m=|a+b|﹣|b﹣1|﹣|a﹣c|,求 1﹣2013(m+c)2013 的值;
(3)若 a=﹣2,b=﹣3,c=![]() ,且 a、b、c 对应的点分别为 A、B、C,问在数轴上是否存在一点 P,使 P 与 A 的距离是 P 与 C 的距离的 3 倍?若存在,请求出 P 点对应的有理数;若不存在,请说明理由.
,且 a、b、c 对应的点分别为 A、B、C,问在数轴上是否存在一点 P,使 P 与 A 的距离是 P 与 C 的距离的 3 倍?若存在,请求出 P 点对应的有理数;若不存在,请说明理由.
![]()
参考答案:
【答案】(1)a<c<|b|;(2)2014;(3) 0 或 2.
【解析】
(1)根据数轴可得 b<0,因此|b|=﹣b,在数轴上表示出﹣b 的位置, 再根据数轴上的数,左边的数总比右边的小可得答案;
(2)首先根据 a、b、c 的位置得到 a+b<0,b﹣1<0,a﹣c<0,然后再把 m=|a+b|﹣|b﹣1|﹣|a﹣c|化简可得 m+c=﹣1,再代入计算出代数式的值即可;
(3)设 P 点对应的有理数为 x,然后分情况讨论:①当点 P 在点 A 的左边时;
②当点 P 在点A 和点 C 之间时;③当点 P 在点 C 的右边时.
(1)如图所示:
a<c<|b|;
(2)由 a、b、c 在数轴上的位置知:a+b<0,b﹣1<0,a﹣c<0, 所以 m=﹣(a+b)+(b﹣1)+(a﹣c),
=﹣a﹣b+b﹣1+a﹣c,
=﹣1﹣c,
所以 m+c=﹣1,
即 1﹣2013(m+c)2013=1﹣2013(﹣1)2013=1+2013=2014;
(3)存在.设 P 点对应的有理数为 x.
①当点 P 在点 A 的左边时,有﹣2﹣x=3(![]() ﹣x),解之得:x=2(不合条件,舍去),
﹣x),解之得:x=2(不合条件,舍去),
②当点 P 在点 A 和点 C 之间时,有 x﹣(﹣2)=3(![]() ﹣x),解之得:x=0,
﹣x),解之得:x=0,
③当点 P 在点C 的右边时,有 x﹣(﹣2)=3 (x﹣![]() ),解之得:x=2,
),解之得:x=2,
综上所述,满足条件的 P 点对应的有理数为 0 或 2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC在平面直角坐标系xOy中的位置如图所示.

(1)作△ABC关于点C成中心对称的△A1B1C1.
(2)将△A1B1C1向右平移4个单位,作出平移后的△A2B2C2.
(3)在x轴上求作一点P,使PA1+PC2的值最小,并写出点P的坐标(不写解答过程,直接写出结果)
-
科目: 来源: 题型:
查看答案和解析>>【题目】“汉十”高速铁路襄阳段正在建设中,甲、乙两个工程队计划参与一项工程建设,甲队单独施工30天完成该项工程的
 ,这时乙队加入,两队还需同时施工15天,才能完成该项工程.
,这时乙队加入,两队还需同时施工15天,才能完成该项工程.
(1)若乙队单独施工,需要多少天才能完成该项工程?
(2)若甲队参与该项工程施工的时间不超过36天,则乙队至少施工多少天才能完成该项工程? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,
, ,
, 点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动,设点D、E运动的时间是t秒
点D从点C出发沿CA方向以每秒2个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒1个单位长的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动,设点D、E运动的时间是t秒 过点D作
过点D作 于点F,连接DE、EF.
于点F,连接DE、EF. 求证:
求证: ;
; 四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由.
四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由. 当t为何值时,
当t为何值时, 为直角三角形?请说明理由.
为直角三角形?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB经过⊙O上的点C,直线AO与⊙O交于点E和点D,OB与⊙O交于点F,连接DF、DC.已知OA=OB,CA=CB,DE=10,DF=6.
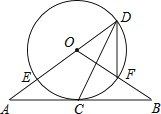
(1)求证:①直线AB是⊙O的切线;②∠FDC=∠EDC;
(2)求CD的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读下面的村料,再分解因式.
要把多项式
 分解因式,可以先把它的前两项分成组,并提出a,把它的后两项分成组,并提出b,从而得
分解因式,可以先把它的前两项分成组,并提出a,把它的后两项分成组,并提出b,从而得 .
.这时,由于
 中又有公困式
中又有公困式 ,于是可提公因式
,于是可提公因式 ,从而得到
,从而得到 ,因此有
,因此有


 .
.这种因式分解的方法叫做分组分解法,如果把一个多项式各个项分组并提出公因式后,它们的另一个因式正好相同,那么这个多项式就可以利用分组分解法来因式分解.
请用上面材料中提供的方法因式分解:

 请你完成分解因式下面的过程
请你完成分解因式下面的过程
 ______
______ ;
; .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】襄阳市某企业积极响应政府“创新发展”的号召,研发了一种新产品.已知研发、生产这种产品的成本为30元/件,且年销售量y(万件)关于售价x(元/件)的函数解析式为:y=
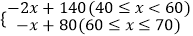 .
.
(1)若企业销售该产品获得的年利润为W(万元),请直接写出年利润W(万元)关于售价x(元/件)的函数解析式;
(2)当该产品的售价x(元/件)为多少时,企业销售该产品获得的年利润最大?最大年利润是多少?
(3)若企业销售该产品的年利润不少于750万元,试确定该产品的售价x(元/件)的取值范围.
相关试题

