【题目】如图,在△ABC中,AB=AC=13厘米,BC=10厘米,AD⊥BC于点D,动点P从点A出发以每秒1厘米的速度在线段AD上向终点D运动,设动点运动时间为t秒.
(1)求AD的长;
(2)当P、C两点的距离为![]() 时,求t的值;
时,求t的值;
(3)动点M从点C出发以每秒2厘米的速度在射线CB上运动.点M与点P同时出发,且当点P运动到终点D时,点M也停止运动.是否存在t值,使得![]() ?若存在,请求出t的值;若不存在,请说明理由.
?若存在,请求出t的值;若不存在,请说明理由.

备用图
参考答案:
【答案】(1)12cm(2)![]() (3)t的值为
(3)t的值为![]() 或
或![]() 或
或![]()
【解析】(1)∵ AB=AC,AD⊥BC;
∴ BD=![]() BC=5cm,且∠ADB=90
BC=5cm,且∠ADB=90![]() .
.
∴![]() .
.
即AD的长为12cm.
(2)AP=t,PD="12" -t,
![]()
又由![]() ,得
,得![]() .
.
解得,![]() .
.
(3)假设存在t,使得S△PMD=![]() S△ABC.
S△ABC.
① 若点M在线段CD上,即![]() 时,PD=12-t,DM=5-2t;
时,PD=12-t,DM=5-2t;
由S△PMD=![]() S△ABC,即
S△ABC,即![]()
![]()
解,得![]() (舍去);
(舍去);![]() . ………………………… 8分
. ………………………… 8分
② 若点M在射线DB上,即![]() .
.
由S△PMD=![]() S△ABC 得
S△ABC 得![]()
![]()
解,得;
![]() . ………………………… 10分
. ………………………… 10分
综上,存在t的值为![]() 或
或![]() 或
或![]() ,使得S△PMD=
,使得S△PMD=![]() S△ABC。(11分)
S△ABC。(11分)
(1)根据勾股定理求得AD的长;
(2)表示出PD=12-t,S△PDC=15,得![]() (12-t)=15,求得t的值即可;
(12-t)=15,求得t的值即可;
(3)假设存在t,使得S△PMD=![]() S△ABC.分两种情况进行讨论:①若点M在线段CD上,②若点M在射线DB上,从而求得t的值;
S△ABC.分两种情况进行讨论:①若点M在线段CD上,②若点M在射线DB上,从而求得t的值;
-
科目: 来源: 题型:
查看答案和解析>>【题目】[发现]如图∠ACB=∠ADB=90°,那么点D在经过A,B,C三点的圆上(如图①)

(1)[思考]如图②,如果∠ACB=∠ADB=a(a≠90°)(点C,D在AB的同侧),那么点D还在经过A, B,C三点的圆上吗?
(2)我们知道,如果点D不在经过A,B,C三点的圆上,那么点D要么在圆O外,要么在圆O内,以下该同学的想法说明了点D不在圆O外。
请结合图④证明点D也不在⊙O外.

[结论]综上可得结论:如图②,如果∠ACB=∠ADB=a(点C,D在AB的同侧),那么点D在经过A,B,C三点的圆上,即:点A、B、C、D四点共圆。
[应用]利用上述结论解决问题:
如图⑤,已知△ABC中,∠C=90°,将△ACB绕点A顺时针旋转一个角度得△ADE,连接BE CD,延长CD交BE于点F,
图⑤
①求证:点B、C、A、F四点共圆;②求证:BF=EF. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的一条弦,C是⊙O上一动点且∠ACB=45°,E、F分别是AC、BC的中点,直线EF与⊙O交于点G、H.若⊙O的半径为2,则GE+FH的最大值为 .

-
科目: 来源: 题型:
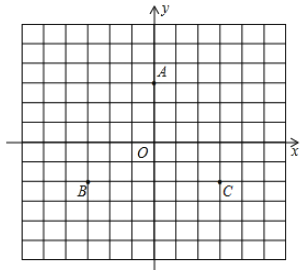
查看答案和解析>>【题目】如图,在直角坐标平面内,点A的坐标是
 ,点B的坐标是
,点B的坐标是
(1)图中点C关于x轴对称的点D的坐标是 .
(2)如果将点B沿着与x轴平行的方向向右平移3个单位得到点
 ,那么
,那么 、
、 两点之间的距离是 .
两点之间的距离是 .(3)求四边形ABCD的面积
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,M、N分别是边AD、BC的中点,点P、Q在DC边上,且PQ=
 DC.若AB=16,BC=20,则图中阴影部分的面积是 .
DC.若AB=16,BC=20,则图中阴影部分的面积是 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】说理填空:如图,点E是DC的中点,EC=EB,∠CDA=120°,DF//BE,且DF平分∠CDA,求证:△BEC为等边三角形.

解: 因为DF平分∠CDA(已知)
所以∠FDC=
 ∠________. ( )
∠________. ( )因为∠CDA=120°(已知)
所以∠FDC=______°.
因为DF//BE(已知)
所以∠FDC=∠_________.(____________________________________)
所以∠BEC = 60°,又因为EC=EB,(已知)
所以△BCE为等边三角形.(_____________________________)
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题
(1)解方程:(x+1)2=9;
(2)解方程:x2﹣4x+2=0.
相关试题

