【题目】已知二次函数y=x2+mx+n的图象经过点P(-3,1),对称轴是经过点(-1,0)且平行于y轴的直线.
(1)求m,n的值;
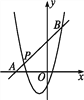
(2)如图,一次函数y=kx+b的图象经过点P,与x轴相交于点A,与二次函数的图象相交于另一点B,点B在点P的右侧,PA∶PB=1∶5,求一次函数的表达式.
参考答案:
【答案】(1)m=2,n=-2;(2)一次函数的表达式为y=x+4.
【解析】试题分析:(1)利用对称轴公式求得![]() ,把
,把![]() 代入二次函数
代入二次函数![]() 进而就可求得
进而就可求得![]() ;
;
(2)根据(1)得出二次函数的解析式,根据已知条件,利用平行线分线段成比例定理求得![]() 的纵坐标,代入二次函数的解析式中求得
的纵坐标,代入二次函数的解析式中求得![]() 的坐标,然后利用待定系数法就可求得一次函数的表达式.
的坐标,然后利用待定系数法就可求得一次函数的表达式.
试题解析:(1)由题意得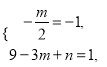 解得
解得![]()
(2)如图,分别过点P,B作x轴的垂线,垂足分别为C,D,则PC∥BD,
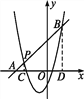
![]() △APC∽△ABD,
△APC∽△ABD,
![]()
![]() .
.
![]() PA∶PB=1∶5,PC=1,
PA∶PB=1∶5,PC=1,
![]()
![]() ,
,
![]() BD=6.
BD=6.
令x2+2x-2=6,
解得:x1=2,x2=-4(舍去),
![]() 点B坐标为(2,6),
点B坐标为(2,6),
![]()
![]() 解得
解得![]()
![]() 一次函数的表达式为y=x+4.
一次函数的表达式为y=x+4.
-
科目: 来源: 题型:
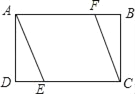
查看答案和解析>>【题目】如图,矩形ABCD中,AD=2,AB=3,过点A,C作相距为2的平行线段AE,CF,分别交CD,AB于点E,F,则DE的长是( )
A.
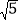 B.
B. 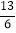 C. 1 D.
C. 1 D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以正方形ABCD的边AB为一边向外作等边△ABE,则∠BED的度数为______.
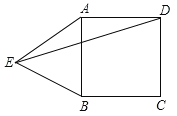
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB=AC,将BC沿BD所在的直线折叠,使点C落在AB边上的E点处.
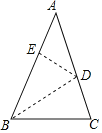
(1)若∠ADE=30°,求∠BDC的度数.
(2)若AB=AC=8,BC=5,求三角形AED的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙两人买了相同数量的信封和信笺,甲每发一封信都只用1张信笺,乙每发一封信都要用3张信笺,结果甲用掉了所有的信封,但余下50张信笺,而乙用掉了所有的信笺,但余下50个信封.
(1)求甲乙两人各买的信封和信笺的数量分别为多少?
(2)若甲乙两人每发出一封信需邮费5元,求甲乙各用去多少元邮费?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是抛物线型拱桥,P处有一照明灯,水面OA宽4 m,从O,A两处观测P处,仰角分别为α,β,且tan α=
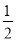 ,tan β=
,tan β= ,以O为原点,OA所在直线为x轴建立平面直角坐标系.
,以O为原点,OA所在直线为x轴建立平面直角坐标系.(1)求点P的坐标.
(2)水面上升1 m,水面宽多少?(结果精确到0.1 m.参考数据:
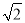 ≈1.41)
≈1.41)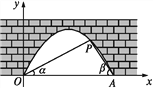
-
科目: 来源: 题型:
查看答案和解析>>【题目】矩形的一角平分线分一边为 3cm 和 4cm 两部分,则这个矩形的对角线的长为_____.
相关试题

