Question

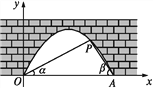
【题目】如图是抛物线型拱桥,P处有一照明灯,水面OA宽4 m,从O,A两处观测P处,仰角分别为α,β,且tan α=,tan β=,以O为原点,OA所在直线为x轴建立平面直角坐标系.

(1)求点P的坐标.

(2)水面上升1 m,水面宽多少?(结果精确到0.1 m.参考数据: ≈1.41)

Answer 1

【答案】（1）点P的坐标为.（2）2.8m.

【解析】试题分析：（1）过点P作PB⊥OA,垂足为B.设点P的坐标为(x,y).运用三角函数可得根据条件可求出，即可得到点的坐标；
（2）若水面上升1m后到达位置，如图，运用待定系数法可求出抛物线的解析式，然后求出时的值，就可解决问题．

试题解析： (1)如图,过点P作PB⊥OA,垂足为B.设点P的坐标为(x,y).

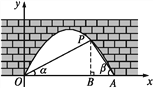
在Rt△POB中,

tan α=,

OB==2y.

在Rt△PAB中,

tan β=,

AB=y.

OA=OB+AB,

即2y+y=4. y=. x=2×=3.

点P的坐标为.

(2)设这条抛物线表示的二次函数为y=ax2+bx.

由函数y=ax2+bx的图象经过(4,0), 两点,可得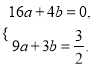

解方程组,得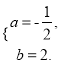

这条抛物线表示的二次函数为y=-x2+2x.

当水面上升1 m时,水面的纵坐标为1,即-x2+2x=1,

解方程,得x1=2-,x2=2+.

x2-x1=2+-(2-)=2≈2.8.

因此,水面上升1 m,水面宽约为2.8 m.