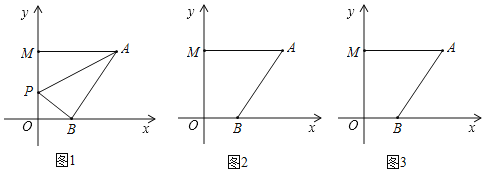
【题目】在平面直角坐标系中,A(6,a),B(b,0),M(0,c),P点为y轴上一动点,且(b﹣2)2+|a﹣6|+![]() =0.
=0.
(1)求点B、M的坐标;
(2)当P点在线段OM上运动时,试问是否存在一个点P使S△PAB=13,若存在,请求出P点的坐标与AB的长度;若不存在,请说明理由.
(3)不论P点运动到直线OM上的任何位置(不包括点O、M),∠PAM、∠APB、∠PBO三者之间是否都存在某种固定的数量关系,如果有,请利用所学知识找出并证明;如果没有,请说明理由.
参考答案:
【答案】(1)M(0,6),B(2,0),A(6,6);(2)AB=2![]() ;(3)①当点P在线段OM上时,结论:∠APB+∠PBO=∠PAM;理由见解析;②当点P在MO的延长线上时,结论:∠APB+∠PBO=∠PAM.理由见解析;③当点P在OM的延长线上时,结论:∠PBO=∠PAM+∠APB.理由见解析;
;(3)①当点P在线段OM上时,结论:∠APB+∠PBO=∠PAM;理由见解析;②当点P在MO的延长线上时,结论:∠APB+∠PBO=∠PAM.理由见解析;③当点P在OM的延长线上时,结论:∠PBO=∠PAM+∠APB.理由见解析;
【解析】
(1)利用非负数的性质,求出a、b、c即可解决问题;
(2)设P(0,m).根据S△PAB=S梯形AMOB-S△APM-S△PBO,构建方程即可解决问题;
(3)分三种情形,分别画出图形解决问题即可.
(1)∵(b-2)2+|a-6|+![]() =0,
=0,
又∵(b-2)2,≥0,|a-6|≥0,![]() ≥0,
≥0,
∴a=6,b=2,c=6.
∴M(0,6),B(2,0),A(6,6),
(2)设P(0,m).
∵S△PAB=13,四边形AMOB是直角梯形,
∴![]() (6+2)6-
(6+2)6-![]() m2-
m2-![]() (6-m)6=13,
(6-m)6=13,
∴m=![]() ,
,
∴P(0,![]() ),
),
AB=![]() =2
=2![]() .
.
(3)①如图2-1中,当点P在线段OM上时,结论:∠APB+∠PBO=∠PAM;
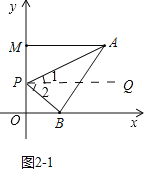
理由:作PQ∥AM,则PQ∥AM∥ON,
∴∠1=∠PAM,∠2=∠PBO,
∴∠1+∠2=∠PAM+∠PBO,
即∠APB=∠PAM+∠PBO,
∠APB+∠PBO=∠PAM;
②如图2-2中所示,当点P在MO的延长线上时,结论:∠APB+∠PBO=∠PAM.
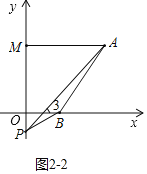
理由:∵AM∥OB,
∴∠PAM=∠3,
∵∠3=∠APB+∠PBO,
∴∠APB+∠PBO=∠PAM.
③如图2-3中,当点P在OM的延长线上时,结论:∠PBO=∠PAM+∠APB.
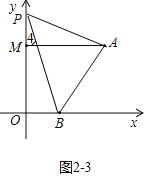
理由:∵AM∥OB,
∴∠4=∠PBO,
∵∠4=∠PAM+∠APB,
∴∠PBO=∠PAM+∠APB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知在平面直角坐标系xOy中,抛物线y1=ax2+bx(a≠0),与x轴正半轴交于点A1(2,0),顶点为P1 , △OP1A1为正三角形,现将抛物线y1=ax2+bx(a≠0)沿射线OP1平移,把过点A1时的抛物线记为抛物线y2 , 记抛物线y2与x轴的另一交点为A2;把抛物线y2继续沿射线OP1平移,把过点A2时的抛物线记为抛物线y3 , 记抛物线y3与x轴的另一交点为A3;….;把抛物线y2015继续沿射线OP1平移,把过点A2015时的抛物线记为抛物线y2016 , 记抛物线y2016与x轴的另一交点为A2016 , 顶点为P2016 . 若这2016条抛物线的顶点都在射线OP1上.
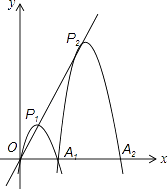
(1)①求△OP1A1的面积;②求a,b的值;
(2)求抛物线y2的解析式;
(3)请直接写出点A2016以及点P2016坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读下列一段文字,再回答问题:
已知平面内两点P1(x1,y1)、P2(x2,y2),这两点间的距离P1P2=
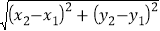 .同时当两点所在的直线在坐标轴上或平行于坐标轴或垂直于坐标轴时,两点间的距离公式可简化为|x2﹣x1|或|y2﹣y1|.
.同时当两点所在的直线在坐标轴上或平行于坐标轴或垂直于坐标轴时,两点间的距离公式可简化为|x2﹣x1|或|y2﹣y1|.(1)已知点A(2,3)、B(4,2),试求A、B两点间的距离;
(2)已知点A、B在平行于x轴的直线上,点A的横坐标为7,点B的横坐标为5,试求A、B两点间的距离;
(3)已知一个三角形的各顶点坐标为A(﹣2,1)、B(1,4)、C(1﹣a,5),试用含a的式子表示△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图,圆P经过点A(﹣4,0),点B(6,0),交y轴于点C,∠ACB=45°,连结AP、BP.

(1)求圆P的半径;
(2)求OC长;
(3)在圆P上是否存在点D,使△BCD的面积等于△ABC的面积?若存在求出点D坐标;若不存在说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图数轴的A、B、C三点所表示的数分别为a、b、c.若|a﹣b|=3,|b﹣c|=5,且原点O与A、B的距离分别为4、1,则关于O的位置,下列叙述何者正确?( )

A.在A的左边
B.介于A、B之间
C.介于B、C之间
D.在C的右边 -
科目: 来源: 题型:
查看答案和解析>>【题目】我们学习了勾股定理后,都知道“勾三、股四、弦五”.
观察:3,4,5;5,12,13;7,24,25;9,40,41;……发现这些勾股数的勾都是奇数,且从3起就没有间断过.
(1)请你根据上述的规律写出下一组勾股数:_______________________;
(2)若第一个数用字母n(n为奇数,且n≥3)表示,则后两个数用含n的代数式表示分别为___________________。
-
科目: 来源: 题型:
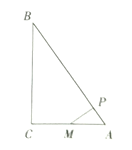
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,AM=CM,MP⊥AB于点P.求证:BP2=AP2+BC2.
相关试题

