【题目】已知在平面直角坐标系xOy中,抛物线y1=ax2+bx(a≠0),与x轴正半轴交于点A1(2,0),顶点为P1 , △OP1A1为正三角形,现将抛物线y1=ax2+bx(a≠0)沿射线OP1平移,把过点A1时的抛物线记为抛物线y2 , 记抛物线y2与x轴的另一交点为A2;把抛物线y2继续沿射线OP1平移,把过点A2时的抛物线记为抛物线y3 , 记抛物线y3与x轴的另一交点为A3;….;把抛物线y2015继续沿射线OP1平移,把过点A2015时的抛物线记为抛物线y2016 , 记抛物线y2016与x轴的另一交点为A2016 , 顶点为P2016 . 若这2016条抛物线的顶点都在射线OP1上.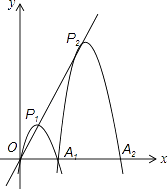
(1)①求△OP1A1的面积;②求a,b的值;
(2)求抛物线y2的解析式;
(3)请直接写出点A2016以及点P2016坐标.
参考答案:
【答案】
(1)
解:①过点P1作作P1B1⊥x轴,垂足为B1.

∵△OP1A1为正三角形,
∴∠P1OA1=60°,P1O=P1A1.
又∵P1B1⊥x轴,
∴0B1=B1A1=1.
∴P1B1=OP1× ![]() =2×
=2× ![]() =
= ![]() .
.
∴P1(1, ![]() ),△OP1A1的面积=
),△OP1A1的面积= ![]() OA1P1B1=
OA1P1B1= ![]() ×2×
×2× ![]() =
= ![]() .
.
②∵将点A1(2,0)、P1(1, ![]() )在抛物线y1上,
)在抛物线y1上,
∴ ![]() ,解得:a=﹣
,解得:a=﹣ ![]() ,b=2
,b=2 ![]()
(2)
解:设直线OP1的解析式为y=kx.
∵将P1(1, ![]() )代入得:k=
)代入得:k= ![]() ,
,
∴直线OP1的解析式为y= ![]() x.
x.
∵点P2在直线OP1上,
∴设点P2(a, ![]() ).
).
∴y2=﹣ ![]() (x﹣a)2+
(x﹣a)2+ ![]() a.
a.
∵将点A1的坐标代入得:﹣ ![]() (2﹣a)2+
(2﹣a)2+ ![]() a=0,解得:a1=1(舍去),a2=4,
a=0,解得:a1=1(舍去),a2=4,
∴y2=﹣ (x﹣4)2+4
![]() ,整理得:y2=﹣
,整理得:y2=﹣ ![]() x2+8
x2+8 ![]() x﹣12
x﹣12 ![]()
(3)
解:∵a2=4,
∴P2(4,4 ![]() ).
).
∴点A1与D点A2关于x=4对称,
∴点A2(6,0).
设P3(b, ![]() )则y3=﹣
)则y3=﹣ ![]() (x﹣b)2+
(x﹣b)2+ ![]() b.
b.
∵将A2(6,0)代入得﹣ ![]() (6﹣b)2+
(6﹣b)2+ ![]() b=0,解得:b1=4(舍去),b2=9,
b=0,解得:b1=4(舍去),b2=9,
∴P3(9,9 ![]() ).
).
∵A2(6,0),点A2与A3关于x=9对称,
∴A3(12,0).
P1(1, ![]() ),A1(2,0),
),A1(2,0),
P2(4,4 ![]() ),A2(6,0),4=22,6=2×3;
),A2(6,0),4=22,6=2×3;
P3(9,9 ![]() ),A3(12,0),9=32,12=3×4;
),A3(12,0),9=32,12=3×4;
…
P2016(4064256,4064256 ![]() ),A2016(4066272,0)
),A2016(4066272,0)
【解析】(1)①过点P1作作P1B1⊥x轴,垂足为B1 . 由等边三角形的性质可知可求得P1B1的长度,然后依据三角形的面积公式可求得△OP1A1的面积;②将点A1(2,0)、P1(1, ![]() )代入抛物线的解析式,即可求得a、b的值;(2)先利用待定系数法求得直线OP1的解析式,然后设点P2(a,
)代入抛物线的解析式,即可求得a、b的值;(2)先利用待定系数法求得直线OP1的解析式,然后设点P2(a, ![]() ).则y2=﹣
).则y2=﹣ ![]() (x﹣a)2+
(x﹣a)2+ ![]() a,接下来,将点A1的坐标代入可求得a的值,从而可得到抛物线的解析式;(3)由a2=4,可求得点P2(4,4
a,接下来,将点A1的坐标代入可求得a的值,从而可得到抛物线的解析式;(3)由a2=4,可求得点P2(4,4 ![]() ),然后依据抛物线的对称性可求得点A2(6,0),接下来,再求得P3(9,9
),然后依据抛物线的对称性可求得点A2(6,0),接下来,再求得P3(9,9 ![]() ),A3(12,0),最后观察所得结果找出其中的规律,依据规律可求得问题的答案.
),A3(12,0),最后观察所得结果找出其中的规律,依据规律可求得问题的答案.
【考点精析】通过灵活运用数与式的规律,掌握先从图形上寻找规律,然后验证规律,应用规律,即数形结合寻找规律即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,设正方体ABCD-A1B1C1D1的棱长为1,黑、白两个甲壳虫同时从点A出发,以相同的速度分别沿棱向前爬行,黑甲壳虫爬行的路线是AA1→A1D1→…,白甲壳虫爬行的路线是AB→BB1→…,并且都遵循如下规则:所爬行的第n+2与第n条棱所在的直线必须既不平行也不相交(其中n是正整数)。那么当黑、白两个甲壳虫各爬行完第2017条棱分别停止在所到的正方体顶点处时,它们之间的距离是( )

A. 0 B. 1 C.
 D.
D. 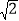
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=2x2﹣x﹣3.
(1)求函数图象的顶点坐标,与坐标轴交点坐标,并画出函数大致图象;
(2)根据图象直接回答:当x为何值时,y<0?当x为何值时y>﹣3? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,在△ABC中,∠B=45°,∠BCA=30°,过点A、B、C三点作⊙O,过点C作⊙O的切线交BA延长线于点D,连接OA交BC于E.

(1)求证:OA∥CD;
(2)求证:△ABE∽△DCA;
(3)若OA=2,求BC的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读下列一段文字,再回答问题:
已知平面内两点P1(x1,y1)、P2(x2,y2),这两点间的距离P1P2=
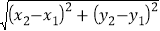 .同时当两点所在的直线在坐标轴上或平行于坐标轴或垂直于坐标轴时,两点间的距离公式可简化为|x2﹣x1|或|y2﹣y1|.
.同时当两点所在的直线在坐标轴上或平行于坐标轴或垂直于坐标轴时,两点间的距离公式可简化为|x2﹣x1|或|y2﹣y1|.(1)已知点A(2,3)、B(4,2),试求A、B两点间的距离;
(2)已知点A、B在平行于x轴的直线上,点A的横坐标为7,点B的横坐标为5,试求A、B两点间的距离;
(3)已知一个三角形的各顶点坐标为A(﹣2,1)、B(1,4)、C(1﹣a,5),试用含a的式子表示△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图,圆P经过点A(﹣4,0),点B(6,0),交y轴于点C,∠ACB=45°,连结AP、BP.

(1)求圆P的半径;
(2)求OC长;
(3)在圆P上是否存在点D,使△BCD的面积等于△ABC的面积?若存在求出点D坐标;若不存在说明理由. -
科目: 来源: 题型:
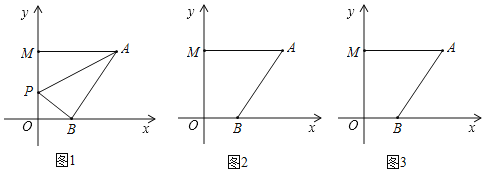
查看答案和解析>>【题目】在平面直角坐标系中,A(6,a),B(b,0),M(0,c),P点为y轴上一动点,且(b﹣2)2+|a﹣6|+
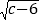 =0.
=0.(1)求点B、M的坐标;
(2)当P点在线段OM上运动时,试问是否存在一个点P使S△PAB=13,若存在,请求出P点的坐标与AB的长度;若不存在,请说明理由.
(3)不论P点运动到直线OM上的任何位置(不包括点O、M),∠PAM、∠APB、∠PBO三者之间是否都存在某种固定的数量关系,如果有,请利用所学知识找出并证明;如果没有,请说明理由.
相关试题

